기숙사 방 배정

넥슨 게임 개발학교는 기숙사를 운영하고있다. 기숙사에는 N명의 학생들이 있다. 학생들은 $1$번부터 $N$번까지 번호가 붙어 있다고 한다. 이들이 잠을 자는 기숙사는 $N$개의 방으로 구성되어 한 명이 방 하나를 쓰도록 되어 있다. 기숙사의 전체 모양은 2진트리 모양이다. 즉, 루트인 방이 하나 있고, 왼쪽과 오른쪽 자식인 방이 각각 존재할 수 있다. 자식인 방이 존재하는 경우 복도로 직접 연결되어 있다. 자식인 방 다음에도 동일한 방식으로 자식인 방들이 존재할 수 있다. 자식 관계의 반대를 부모라고 부른다.

어느 날 교장선생님은 학생들이 잠을 잘 방을 다음과 같은 “규칙1”에 따라 배정하도록 지시하였다.

규칙1: 루트의 왼쪽 자식과 그 연결된 방들의 수가 $i$개이면, $1$번부터 $i$번 학생의 방을 왼쪽 자식과 그 연결된 방들에 배정하고, 루트에는 $i+1$번을 배정하며, 루트의 오른쪽 자식과 그 연결된 방들에 $i+2$번부터 $N$번까지의 학생들을 배치한다. 모든 방에 루트와 동일한 규칙을 재귀적으로 적용한다.

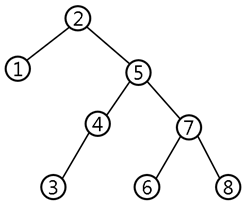
전달 실수로 학생들은 다음과 같은 “규칙2”에 따라 방을 배정하고 말았다.

규칙2: 루트의 왼쪽 자식과 그 연결된 방들의 수가 $i$개이면, $1$번부터 $i$번 학생의 방을 왼쪽 자식과 그 연결된 방들에 배정하고, 루트의 오른쪽 자식과 그 연결된 방들에 $i+1$번부터 $N-1$번까지의 학생들을 배치하며, 루트에는 $N$번을 배정한다. 모든 방에 루트와 동일한 규칙을 재귀적으로 적용한다.

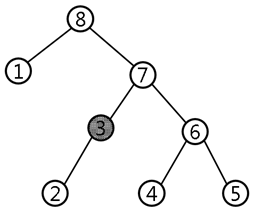
규칙 2에 따라 방을 배정한 결과는 위와 같을 것이다. 교장 선생님은 연락이 잘못된 것을 알고 원래 규칙1대로 모두 방을 옮기도록 하였다. 하지만, 몇몇 학생들은 이미 잠이 들어 버려서 방을 옮길 수가 없었다. (위의 예에서는 3번 학생이 잠이 들었다.) 학생들은 할 수 없이, 잠든 학생들을 그대로 둔 상태로 나머지 학생들만 규칙1을 적용하여 방을 옮기는 것으로 실행했다. 잠든 학생들이 방을 옮기지 않은 상태에서 규칙1을 적용하는 것은 다음과 같이 실행했다고 한다.

규칙3: 잠들지 않은 학생들은 규칙1에 따라 방이 배정되는 학생의 번호 순서대로 작은 번호의 학생들부터 방을 배정받는다. 단, 잠든 학생이 있는 방이 있는 경우 그 방을 건너뛰고 같은 순서를 유지하여 방을 배정받는다.

이 규칙은 잠든 학생이 없는 경우 규칙1과 같은 결과를 만들어 낸다는 것을 알 수 있다. 하지만 위의 예와 같이 한명의 잠든 학생이 있는 경우 다음과 같은 결과가 됨을 알 수 있다.

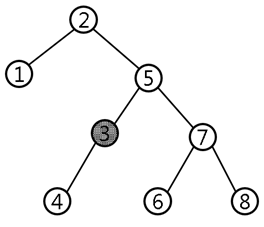
기숙사의 방의 배치와, 잠든 학생들의 번호를 입력으로 받아서 규칙2로 배치된 상태에서 규칙3으로 배치된 상태로 이동하기 위해 각 학생이 지나야 하는 최소 복도의 개수의 합을 계산하는 프로그램을 작성하라.

입력 형식

첫째 줄에 방의 개수를 나타내는 자연수 $N$과 잠든 학생의 수를 나타내는 $K$가 주어진다. ($1 \le N \le 100\,000$, $0 \le K \le N$)

둘째 줄에 방들의 연결 상태가 다음의 규칙으로 주어진다. 우선 루트는 항상 존재하므로 루트가 존재하는지의 여부는 주어지지 않는다. 루트부터 시작하여 존재하는 방들에 대해 레벨 순서로, 왼쪽과 오른쪽 자식의 존재 여부가 각각, 순서대로 0 혹은 1로 주어진다. 1인 경우 자식이 존재한다는 것이다. 레벨 순서란 루트에 가까운 방들이 우선하고, 루트에서 거리가 같은 경우 왼쪽부터 정한 순서를 의미한다.

세번째 줄에 $K$개의 잠든 학생의 번호가 주어진다. 주어지는 학생의 번호는 모두 다르다. $K=0$인 경우 세번째 줄은 빈 줄로 주어진다. 입력 방식에 대해서, 아래의 입력 예의 첫번째 경우가 그림의 예제에 해당하는 것이므로 주의 깊게 살펴보라.

출력 형식

첫 줄에 각 학생이 지나야 하는 최소 복도의 개수의 합을 출력한다.

예제 1

8 1
1 1 0 0 1 1 1 0 1 1 0 0 0 0 0 0
3

14

예제 2

2 1
0 1 0 0
2

0

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설