개구리 한 마리가 강가에 있다. 개의 통나무가 떠 있다. 통나무들 중에는 개구리가 가고 싶어하는 목적지 통나무가 하나 있다. 강과 통나무를 차원 좌표 평면에 표시하기로 하자. 개구리는 축 위에서 시작하여 상하로 뛰어서 통나무들 간을 움직일 수 있다. 한번 축 위를 떠나면, 개구리는 통나무 위에만 위치할 수 있다.
통나무는 좌우 방향으로 긴 형태이고 오른쪽으로 움직인다. 통나무들의 크기는 서로 다를 수 있으며, 움직이는 속도와 움직이기 시작하는 시점도 다를 수 있다. 좌표 값이 인 위치부터, 좌표 값이 인 위치까지 모든 위치에 통나무가 하나씩 있다.
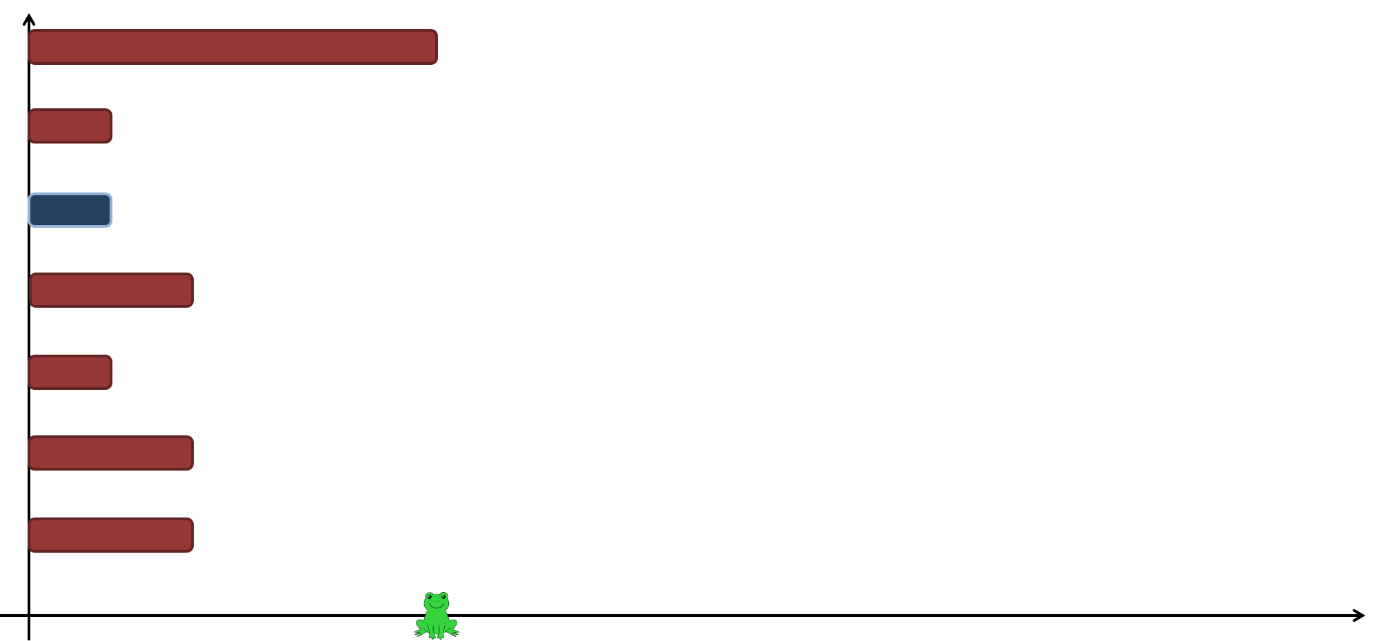
처음에 통나무는 모두 축에 왼쪽 끝이 닿은 위치에 있다. 다음 그림은 처음에, 즉 초에 개구리와 통나무가 어떻게 위치하는지 보여준다. 색이 다른 통나무 하나가 목적지이다.
개구리가 점프할 수 있는 거리는 로 주어진다. 즉, 현재 위치에서 상하 거리가 이내인 통나무로 이동할 수 있다. 개구리는 현재 위치한 통나무에서 상하 방향으로 점프해서 거리가 이내인 어떤 통나무로든 한번에 점프할 수 있다. 현재 위치한 통나무와 점프하려는 통나무는 동일한 좌표의 점을 최소 개는 공유해야 한다. 즉 두 통나무는 아래에서 봤을 때 일부가 겹치거나 적어도 끝 점이 닿아 있어야 한다. 처음 축에서 떠날 때는 거리가 이내인 아무 통나무로든 점프가 가능하다. 개구리는 매 초 한번씩 상하로 뛸 수 있다. (가만히 있을 수도 있다.)
개구리가 좌우로 움직이는 것은 언제든 가능하다. 좌우로 움직이는 데는 시간이 전혀 걸리지 않는 것으로 생각하자. 초에 개구리는 움직일 수 없다. 다음은 초에 통나무들이 움직인 것을 보여 준다.
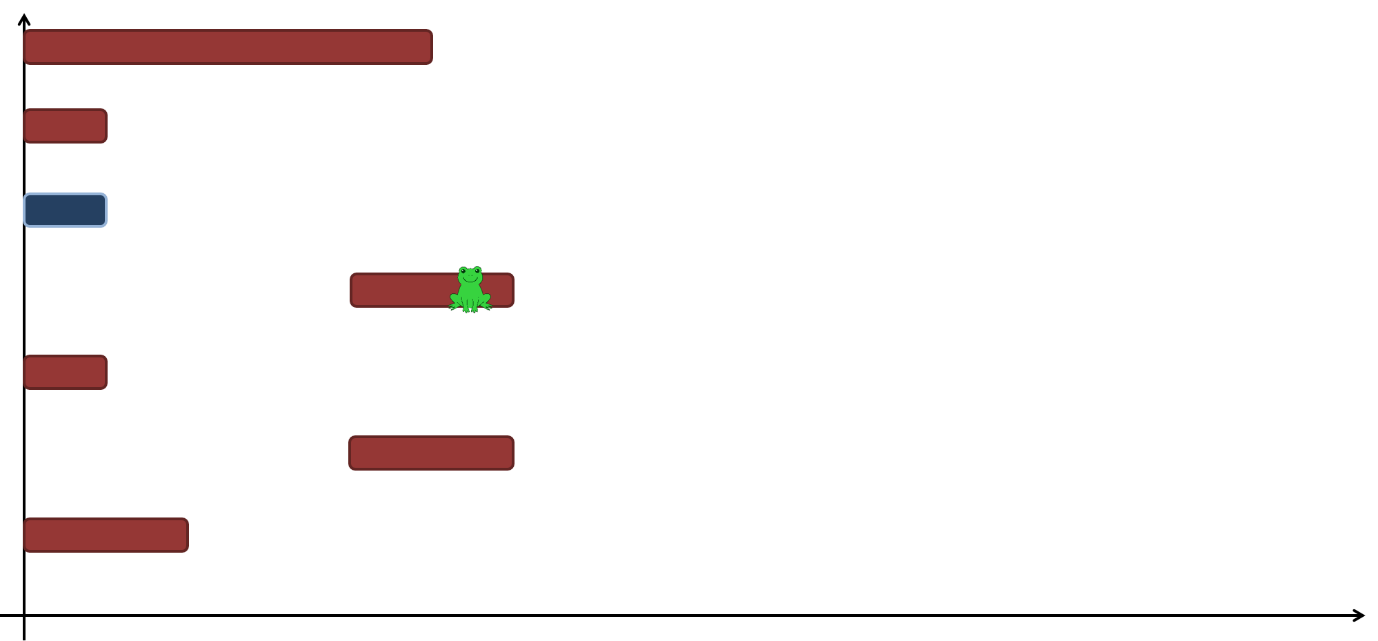
통나무들 중 개가 움직이기 시작했다. 각 통나무는 한번 움직이기 시작하면 동일한 속도로 계속 움직인다. 통나무는 초에 한번씩 순간이동 하는 것으로 생각하자.
이 예에서 이다. 개구리는 초 시점에 아래쪽 개의 통나무들 중 어디든 갈 수 있다. 지금은 아래에서 번째 통나무로 점프했다.
다음은 초 시점을 보여 준다.
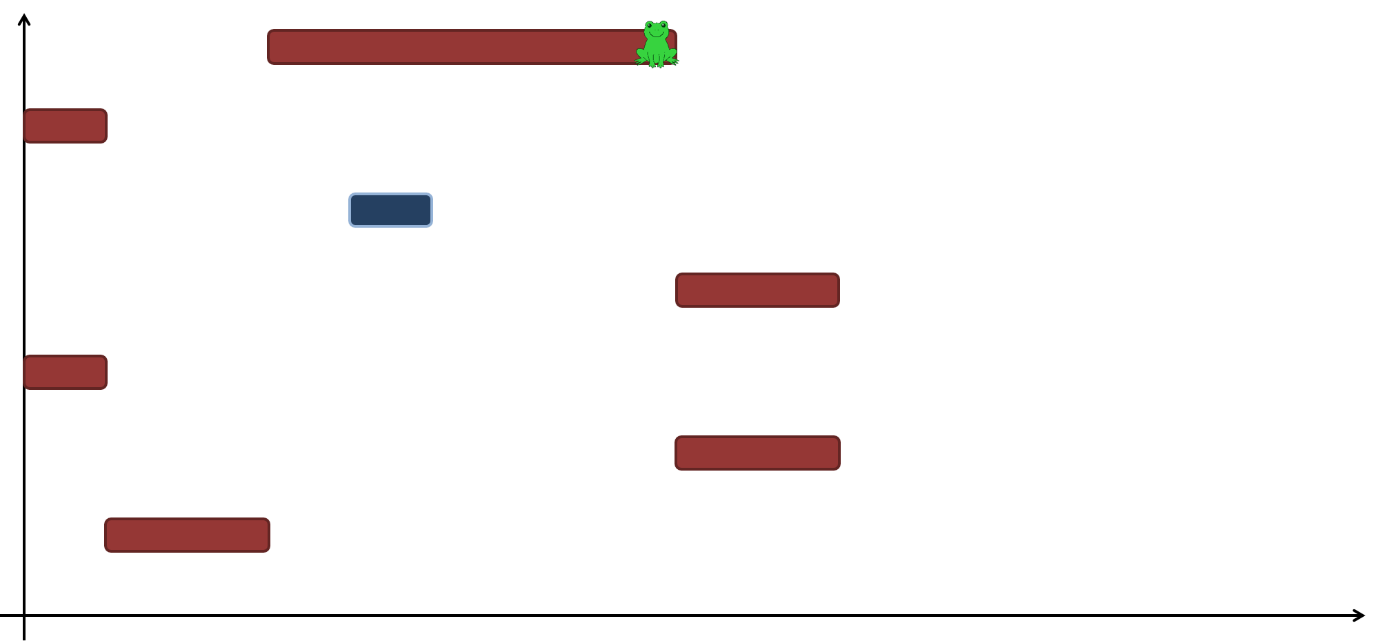
통나무들 중 개가 또 움직이기 시작했다. 개구리는 아래에서 번째 통나무로 점프했다. 아래에서 번째 통나무와 아래에서 번째 통나무는 끝점이 동일한 좌표에 있기 때문에 점프가 가능하다. 지금 시점에서 아래에서 번째 통나무에서 목적지 통나무로는 점프가 불가능하다.
아래는 초 시점이다.
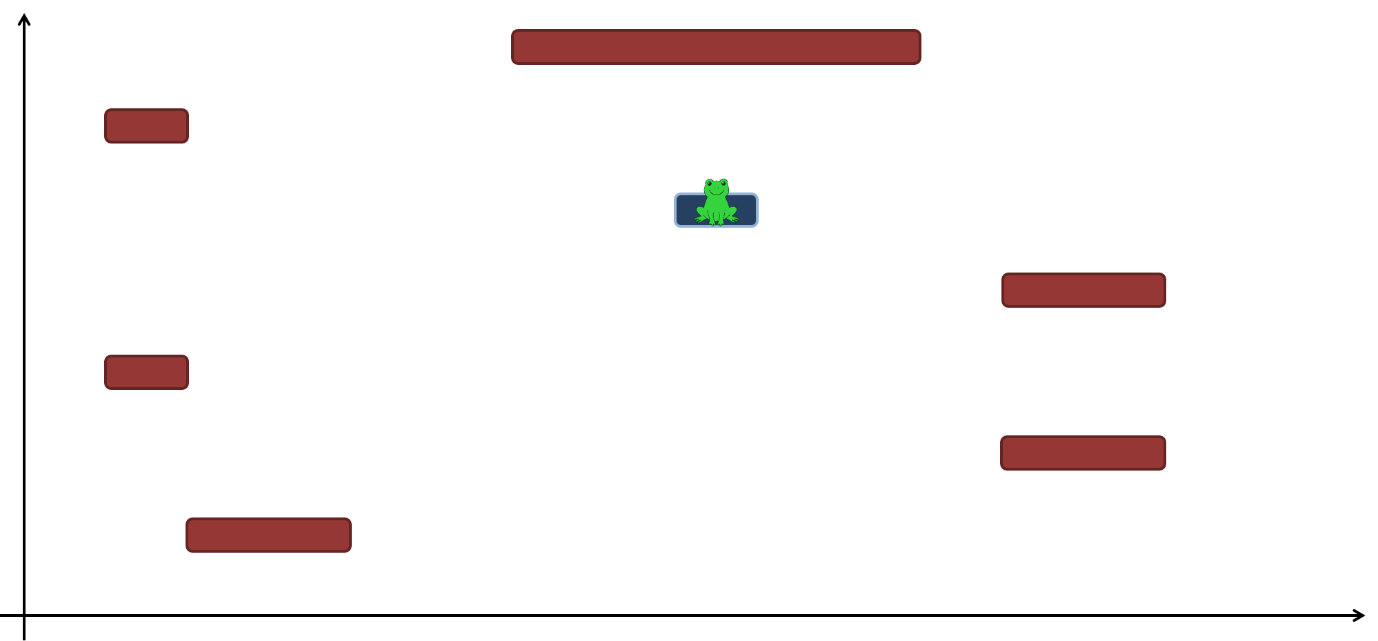
입력 형식
첫째 줄에 통나무의 개수를 나타내는 자연수 과 목적지 통나무의 좌표를 나타내는 자연수 , 그리고 점프할 수 있는 거리 가 공백으로 구분되어 주어진다. (, )
둘째 줄부터 개의 줄에 좌표가 작은 것부터 한 줄에 하나씩, 통나무의 크기, 움직이기 시작하는 시점, 움직이는 속도가 개의 자연수로 공백으로 구분되어 주어진다. 이 때 주어지는 자연수는 보다 크지 않다.
출력 형식
첫 줄에 개구리가 가장 빨리 도착할 수 있는 시점을 자연수로 출력한다. 만약, 목적지 통나무에 도착할 수 없으면 -1을 출력한다.
예제
입력
7 5 4 2 2 1 2 1 4 1 3 1 2 1 4 1 2 4 1 3 1 5 2 3
출력
3
채점 방식
입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.
종류 1: 50점
종류 2: 100점
종류 2: 200점
문제의 원래 제한조건 이외의 추가된 제한이 없음.