파란색 영역

하얀 도화지 위($2$차원 평면)에 파란색 크레파스로 $x$축과 $y$축에 평행한 변을 가진 정사각형을 그려서 내부를 모두 파란색으로 칠한다. 결과적으로 이 정사각형의 테두리와 내부 모두를 포함하는 영역이 파란색으로 칠해짐을 알 수 있다.

이렇게 그린 $N$개의 파란색 정사각형들이 평면 상에 놓여 있다. 각 정사각형은 왼쪽/아래 꼭지점의 좌표와 변의 길이로 나타낸다. 이 때, 파란색의 연결된 영역들이 몇 개 생기는지 그 개수를 출력하는 프로그램을 작성하시오.

여기서, 파란색의 연결된 영역이란 이 영역의 임의의 두 점 $a$, $b$에 대해서, 개미가 $a$에서 출발해서 파란색 영역만을 지나서 $b$에 도착할 수 있는 경로가 적어도 하나 존재한다는 것을 의미한다. 정사각형의 변이 $x$축과 $y$축에 평행하다는 사실을 이용해서 파란색의 연결된 영역 $P$를 다시 정의할 수 있다. $P$에 속하는 임의의 두 점 $a$, $b$에 대해서, $a$와 $b$를 연결하고 파란색 영역에 놓여있는 $x$축과 $y$축에 평행한 선분들로 이루어진 경로가 적어도 하나 존재한다.

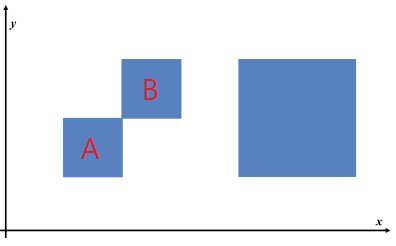
아래 그림에서 각각 왼쪽/아래 꼭지점 $(1, 1)$과 $(2, 2)$를 가지는 변의 길이 $1$인 두 정사각형과 왼쪽/아래 꼭지점 $(4, 1)$을 가지는 변의 길이 $2$인 정사각형이 주어진다. 여기서 왼쪽의 두 정사각형을 $A$와 $B$라고 하면, $A$와 $B$는 점 $(2, 2)$에서 만나고 정사각형 영역은 테두리를 포함하므로 두 정사각형은 하나의 파란색 영역을 정의한다. 다시 말해서, $A$안의 임의의 점 $a$와 $B$안의 임의의 점 $b$를 생각하면, $x$축과 $y$축에 평행한 선분들로 이루어지고 파란색 영역에 놓여있는 $a$와 $b$를 연결하는 경로 $P$가 존재한다. 분명 경로 $P$는 점 $(2, 2)$를 지난다. 따라서 이 그림의 경우 파란색의 연결된 영역은 $2$개 생긴다.

입력 형식

첫 번째 줄에는 정사각형의 개수 $N$이 주어진다. ($1 \le N \le 1\,000$)

다음 $N$개의 줄에는 세 개의 정수 $a$, $b$, $L$이 주어진다. ($0 \le a, b \le 10^9$, $1 \le L \le 10^9$) 여기서 $a$와 $b$는 한 정사각형의 왼쪽 아래 꼭짓점의 좌표가 $(a, b)$라는 것을 나타내고, $L$은 이 정사각형의 한 변의 길이를 나타낸다. 모든 정사각형의 꼭짓점은 $x$좌표와 $y$좌표가 각각 $10^9$ 이하이다.

출력 형식

첫 줄에 파란색의 연결된 영역들의 개수를 출력한다.

예제 1

3
1 1 1
2 2 1
4 1 1

2

예제 2

5
1 1 2
2 2 2
4 1 1
5 2 1
5 2 2

1

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설