개미와 보도 블록

개미가 2차원 평면의 어떤 시작점에서 목적지로 이동하려고 한다. $2$차원 평면에는 보도블록이 아래와 같은 형태로 엇갈려서 깔려 있다. 그림에서 선은 보도 블록의 경계를 나타내며 동일한 무늬가 무한히 반복된다. 일부 점들에 대한 좌표가 주어져 있으니 참고하라.

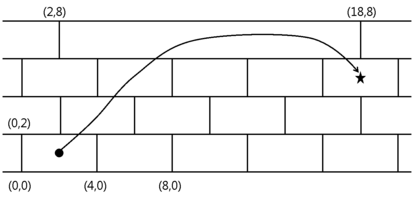
일부 세로 경계는 흙으로 메워져서 없는 것과 완전히 동일한 상태가 되었다. 위의 그림에서는 좌표가 $(2, 8)$인 곳과 좌표가 $(18, 8)$인 곳을 잇는 가로 경계 아래에 있는 $3$개의 세로 경계가 없어졌음을 알 수 있다. 개미는 보도의 경계를 넘는 것을 힘들어하기 때문이 최소 개수의 경계를 넘어서 목적지에 가고 싶다. 위의 그림에서는 $4$개의 경계를 넘어가는 방법이 있음을 알 수 있다.

세로 경계가 없어진 곳의 위치들과, 출발지, 목적지의 좌표를 입력으로 받아 출발지에서 목적지로 가는 길에서 최소로 넘을 수 있는 경계의 개수를 구하는 프로그램을 작성하시오.

입력 형식

첫째 줄에 없어진 세로 경계의 개수를 나타내는 정수 $N$이 주어진다. ($0 \le N \le 3\,000$)

둘째 줄부터 $N$개의 줄에 걸쳐 없어진 세로 경계의 중점 좌표가 하나씩 주어진다.

다음 줄에 출발지의 좌표가 주어지고, 그 다음 줄에 목적지의 좌표가 주어진다. 모든 좌표 값은 $-100\,000\,000$ 이상, $100\,000\,000$ 이하의 정수이다. 출발지와 목적지가 존재하는 경계 위에 있는 경우는 없다.

출력 형식

첫 줄에 출발지에서 목적지로 가는 동안 넘을 수 있는 최소 경계 수를 출력한다.

예제 1

3
6 7
10 7
14 7
2 1
18 5

4

예제 2

0
2 1
18 5

5

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설