칠하기

$2$차원 평면에 단조직교다각형이 주어진다. 이 문제에서 단조직교다각형은 모든 꼭짓점이 정수 좌표를 가지고, 모든 변은 수직 혹은 수평이며, 어떤 수직인 직선을 그었을 때 꼭짓점이 아닌 곳에서 만나는 다각형의 수평인 변이 최대 $2$개인 것을 말한다. 예를 들어, 아래 그림의 왼쪽은 단조직교다각형이지만 오른쪽은 단조직교다각형이 아니다.

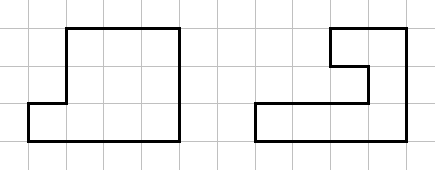
주어진 다각형의 내부를 모두 칠하려고 한다. 칠을 하기 위해서 밑면이 한 변의 길이가 $1$인 정사각형이고 높이가 $2$인 정사각기둥을 사용한다. 아래 그림은 다각형의 내부의 한 위치에 밑면이 닿아있는 상태인 정사각기둥을 왼쪽으로 눕히는 과정을 보여준다.

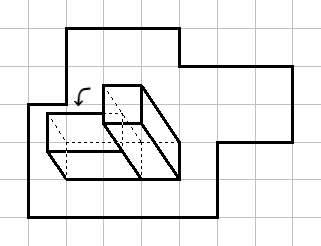
초기에 정사각기둥은 위 그림처럼 밑면이 다각형 내부에 닿아 있을 수도 있고, 옆면이 다각형 내부에 닿아 있을 수 있다. 이때 정사각기둥의 꼭짓점은 항상 정수 좌표인 위치에 있어야 한다.

다각형을 칠하는 방법은, 초기 상태에서 시작하여 정사각기둥을 상하좌우로 눕히거나, 세우거나, 옆으로 굴리는 것을 반복하는 것이다. 다각형에 정사각기둥의 면이 닿은 부분은 색이 칠해진다. 이미 색이 칠해진 부분을 다시 칠하는 것은 상관없다. 하지만, 칠하는 과정 중에서 어떤 순간에도 정사각기둥이 다각형의 밖에 닿아서는 안 된다.

아래 예에서 동일한 단조직교다각형에 대해서 시작 상태 3가지를 보였다. 정사각기둥이 다각형에 닿은 부분이 동일하면 정사각기둥의 다른 면이 닿아 있어도 동일한 시작 상태로 간주한다. 제일 왼쪽 초기 상태에서는 다각형 내부를 모두 칠할 수 없지만, 나머지 두 가지 초기 상태에서는 다각형 내부를 모두 칠할 수 있음을 알 수 있다.

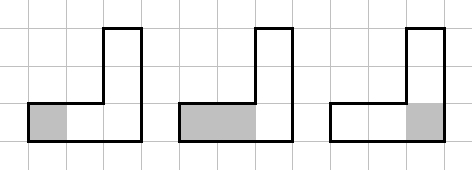
단조직교다각형을 입력으로 받아 다각형 내부를 모두 칠할 수 있는, 정사각기둥의 시작상태의 개수를 출력하는 프로그램을 작성하시오.

입력 형식

단조직교다각형은 입력의 편의를 위해서 다각형을 왼쪽부터 직사각형으로 분할하여 주어진다.

첫 번째 줄에는 분할된 직사각형의 개수 $N$이 주어진다. ($1 \le N \le 20\,000$)

다음 $N$개의 줄 각각에는 세 정수 $H$, $W$, $Y$가 주어진다. $H$는 직사각형의 세로 길이, $W$는 직사각형의 가로 길이, $Y$는 직사각형의 아래 변이 $x$축에서 떨어진 거리이다. 이어져 주어진 두 직사각형에서 첫 번째 직사각형의 오른쪽 변과 두 번째 직사각형의 왼쪽 변이 겹치는 길이가 $1$ 이상임이 보장된다. ($1 \le H, W \le 10\,000$, $0 \le Y \le 10\,000$)

출력 형식

다각형 내부를 모두 칠할 수 있는 정사각기둥의 시작상태의 개수를 출력한다.

예제 1

2
1 2 0
3 1 0

3

예제 2

1
2 4 0

10

예제 3

2
2 2 0
2 2 1

0

예제 4

2
2 3 0
2 3 1

16

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설