카트 발사

배찌와 다오는 $2$차원 평면상에 $N$개의 꼭짓점으로 구성된 수평선분과 수직선분이 한 번씩 번갈아 가며 이어진 경계선으로 이루어진 직교 다각형 트랙에서 경주했다.

이 트랙의 모든 꼭짓점은 서로 다르며, 연속한 두 변 이외에는 어떤 두 변도 만나지 않는다.

결승전 직전까지 다오가 이기고 있었지만, 마지막 순간 부스터가 모자랐던 다오는 배찌에게 역전당했다.

패배해서 화가난 다오는 타고 있던 카트를 그대로 발사시켜버렸다. (아래 이미지를 참고해주시면 좋다.)

카트는 트랙 안의 점 $(\mathit{sx}, \mathit{sy})$에서 시작해서 초당 $x$ 좌표가 $\mathit{dx}$ 만큼, $y$ 좌표가 $\mathit{dy}$ 만큼 이동한다. 점 $(\mathit{sx}, \mathit{sy})$는 트랙의 변 위에 없음은 보장된다.

발사된 카트는 트랙의 경계선을 만났을 때 튕겨져 나오면서 방향을 바꾸는데, 이때 입사각과 반사각이 같다. 만약 카트가 트랙의 꼭짓점에 부딪혔을 때는 왔던 방향으로 방향을 바꾼다.

발사된 카트는 $x$가 감소하는 방향을 바라보게 되는 순간 즉시 멈추게 된다. 처음 카트는 벽 위에 없고, $x$가 증가하는 방향으로 발사됨이 보장된다.

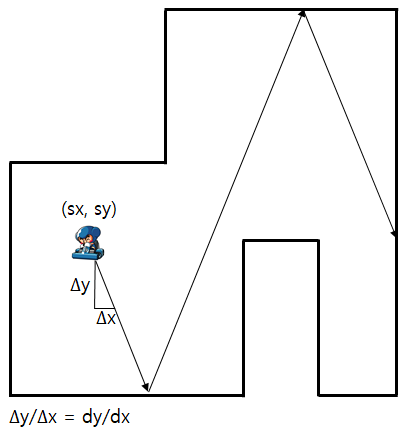
다오는 자기가 발사시킨 카트가 얼마나 오른쪽으로 이동했는지 궁금해졌다. 다오를 도와 카트가 이동한 x축 방향 거리를 계산해주자.

입력 형식

첫 번째 줄에 트랙의 꼭짓점을 이루는 점의 개수 $N$, 초기 카트의 위치 $\mathit{sx}$, $\mathit{sy}$, 초기 카트가 발사되는 방향 $\mathit{dx}$, $\mathit{dy}$가 공백으로 구분되어 주어진다. ($4 \le N \le 200\,000$; $-10^9 \le \mathit{sx}, \mathit{sy}, \mathit{dy} \le 10^9$; $0 < \mathit{dx} \le 10^9$)

그다음 $N$개의 줄에 걸쳐 트랙을 이루는 꼭짓점 $x_i$, $y_i$가 시계방향 혹은 반시계방향으로 입력으로 주어진다. ($-10^9 \le x_i, y_i \le 10^9$)

입력으로 주어지는 다각형은 직교다각형임이 보장되며, 모든 입력되는 수는 정수이다.

출력 형식

다오가 발사한 카트가 이동한 $x$축 거리를 첫 줄에 출력하라.

예제

10 2 3 2 -5
1 1
4 1
4 3
5 3
5 1
6 1
6 6
3 6
3 4
1 4

4

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설