하노이 타워

$N$ 개의 크기가 모두 다른 원판과 $3$ 개의 기둥이 있는 하노이 타워 게임을 생각해 보자. 기둥들은 $1$, $2$, $3$번으로 번호가 붙어 있다. 이 게임의 상태란 $N$ 개의 원판이 임의의 기둥에 위치할 수 있는 것을 말한다. 단, 큰 원판이 작은 원판의 위에 있는 것은 허용하지 않는다. 즉, 한 기둥에 있는 원판들의 집합이 정해지면 그 순서는 저절로 정해진다.

하노이 타워의 상태 $A$와 $B$가 있다고 하면, $A$에서 $B$로의 최단 거리 이동은 아래와 같이 정해진다.

1. 처음의 상태는 $A$이고, 모든 작업이 끝난 후의 상태는 $B$이다.
2. 한 번의 작업에서 하나의 원판만 한 기둥에서 다른 기둥으로 옮길 수 있다.
3. 원판을 옮길 때 큰 원판이 작은 원판의 위로 올라가는 것은 허용되지 않는다.
4. 전체 작업에서 움직이는 원판 중 가장 큰 것은 한 번만 움직일 수 있다.

모든 원판 중 가장 큰 것이 아니라 움직이는 원판 중 가장 큰 것이 한 번만 움직여야 한다는 것에 주의하라. 다른 원판들은 몇 번을 움직여도 상관이 없다.

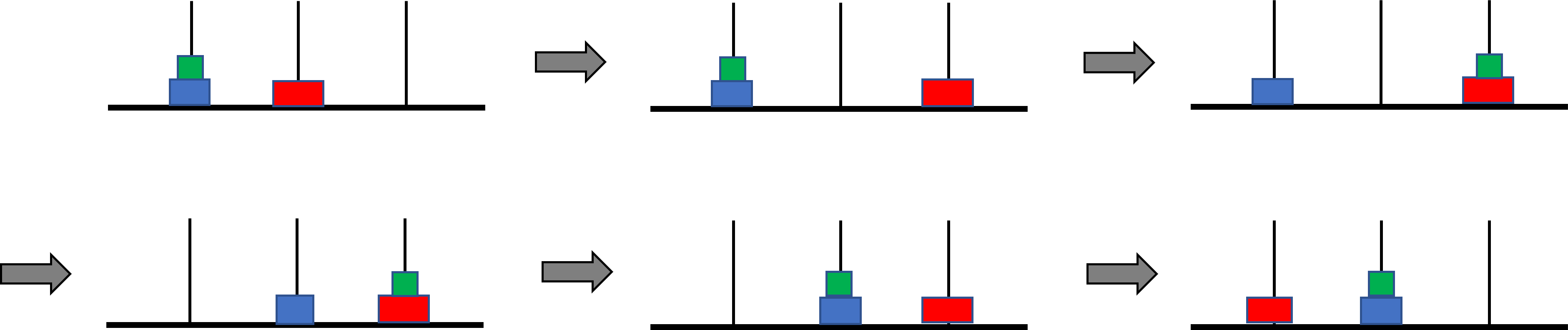
아래 예들에는 3개의 원판이 있고, 빨간 색이 가장 큰 원판, 파란 색이 두번째 큰 원판, 녹색이 가장 작은 원판이다. 그림 1에서 보인 것 처럼, 첫 상태에서 마지막 상태로 이동하는 것은 다섯 번의 작업으로 가능하다. 하지만, 움직이는 원판 중 가장 큰 원판이 두 번 움직였으므로 이 문제에서는 허용되지 않는 방법이다.

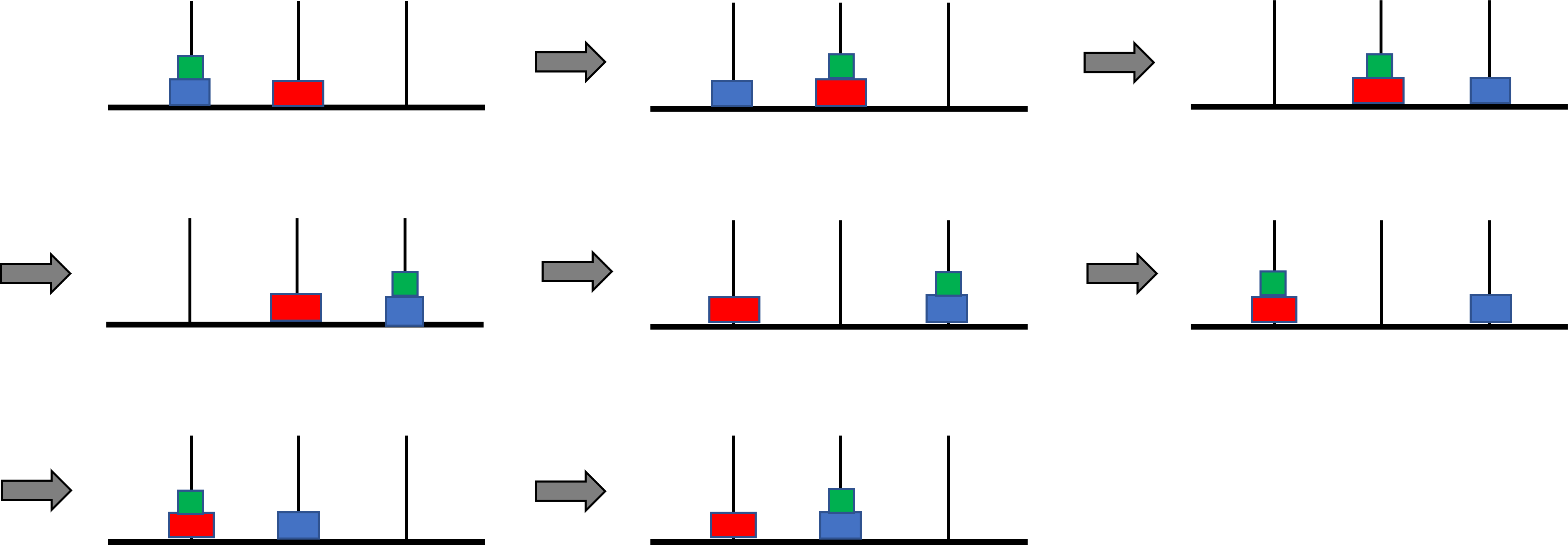
이 문제에서 가능한 최단 거리 이동은 아래 그림과 같이 일곱 번의 작업을 사용하는 것이다.

하노이 타워의 상태 $4$개, $A$, $B$, $C$, $D$를 입력으로 받아 $A$에서 $B$로의 최단 거리 이동에 등장하는 모든 상태와, $C$에서 $D$로의 최단 거리 이동에 등장하는 모든 상태 중 공통으로 등장하는 것들의 개수를 계산하는 프로그램을 작성하라. 상태들 $A$, $B$, $C$, $D$도 공통으로 등장하면 포함해야 한다.

입력 형식

첫 줄에 원판의 개수를 나타내는 정수 $N$이 주어진다. ($1 \le N \le 300\,000$)

그다음 네 개의 줄에 걸쳐 상태 $A$, $B$, $C$, $D$를 나타내는 길이 $N$인 문자열이 한 줄에 하나씩 주어진다. 각 문자열은 1, 2, 3으로 이루어져 있고, 문자열의 각 문자는 작은 원판부터 각 원판이 위치한 기둥의 번호를 나타낸다.

출력 형식

공통으로 등장하는 상태의 개수를 $10^{9} + 7$로 나눈 나머지를 출력한다.

예제 1

3
112
221
131
321

2

예제 2

4
2113
2323
2113
2323

5

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설