파스칼 삼각형

파스칼 삼각형은 다음과 같은 성질을 만족하는 수로 이루어진 정삼각형이다.

• 첫 줄에는 수가 하나, 둘째 줄에는 수가 둘, 셋째 줄에는 수가 셋,... $n$ 번째 줄에는 수가 $n$ 개 있다.
• 각 줄의 맨 처음 수와 맨 마지막 수는 $1$이다.
• 줄은 무한히 많이 있고, $n$ 번째 줄의 $i$ ($1 \lt i \lt n$) 번째 수는 바로 윗 줄의 $i-1$ 번째 수와 $i$ 번째 수의 합이다.

예를 들어, 파스칼 삼각형의 첫 여섯 줄을 나타내면 다음과 같다.

이제 파스칼 삼각형의 특정한 위치 하나 (예를 들어, $a$ 번째 줄 $b$ 번째 수라고 하자)를 고른 다음, 이 위치의 수가 꼭짓점이 되는 크기가 $c$인 정삼각형을 다음과 같이 정의하자.

• 삼각형의 세 꼭짓점은 $a$ 번째 줄 $b$ 번째 수, $a+c-1$ 번째 줄 $b$ 번째 수, $a+c-1$ 번째 줄 $b+c-1$ 번째 수이다. ($c \ge 1$)
• 편의상 가장 위의 꼭짓점과 삼각형의 크기로 정삼각형을 표현하기로 한다.

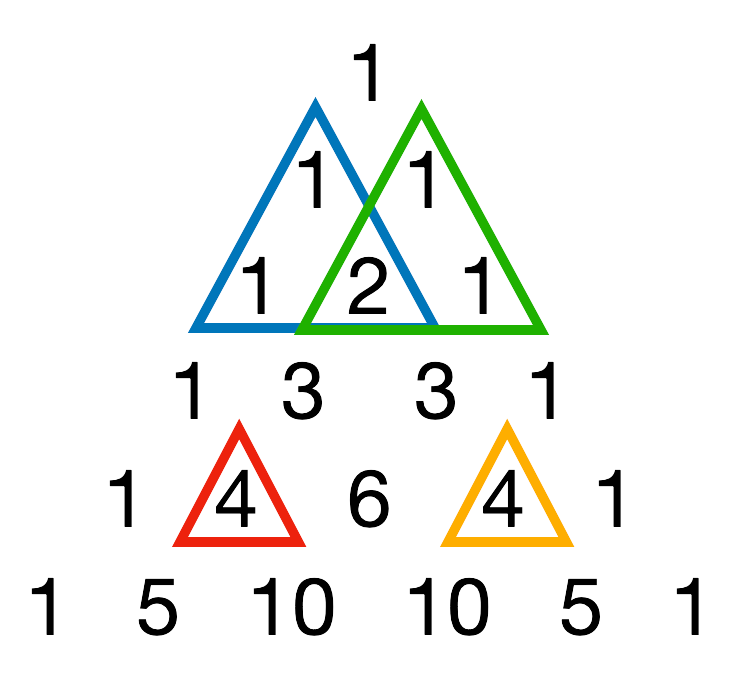
<그림 2>를 보자. $2$ 번째 줄 $1$ 번째 수가 한 꼭짓점인 크기 $2$인 정삼각형은 파란색으로, $2$ 번째 줄 $2$ 번째 수가 한 꼭짓점인 크기 $2$인 정삼각형은 초록색으로, $5$ 번째 줄 $2$ 번째 수가 한 꼭짓점인 크기 $1$인 정삼각형은 빨간색으로, $5$ 번째 줄 $4$ 번째 수가 한 꼭짓점인 크기 $1$인 정삼각형은 노란색으로 표시되어 있다.

이제 정삼각형 안의 수들의 합은 삼각형 안에 있는 수의 합이다. 예를 들어 <그림 2>의 경우 정삼각형 안의 수의 합은 모두 $4$이다.

무한한 크기의 파스칼 삼각형에 대해 다음과 같은 질의를 하려고 한다. 이 삼각형에 포함되는 정삼각형 중 안의 수의 합이 정확하게 $K$인 경우는 모두 몇 가지인가? $K$가 주어질 때 이 질의를 답하라.

입력 형식

첫 줄에 질의의 수를 나타내는 정수 $T$가 주어진다. ($1 \le T \le 4\,000$)

그 다음 $T$ 개의 줄에 걸쳐 각 질의를 나타내는 정수 $K$가 주어진다. ($1 \le K \le 10^{18}$)

출력 형식

$T$ 개의 줄에 걸쳐, 무한한 크기의 파스칼 삼각형에서 정삼각형 안의 수들의 합이 정확하게 $K$인 경우의 수를 출력한다. 만약 이러한 삼각형이 무수히 많다면, $-1$을 출력한다.

예제

3
1
2
3

-1
1
3

예제 설명

잘 생각해보면 정삼각형 내부의 수의 합이 $1$인 경우는 무수히 많음을 알 수 있고, 이 때 답은 $-1$이다. 정삼각형 내부의 수의 합이 $2$인 경우는 둘째 줄의 $2$ 하나로 이루어지는 정삼각형 뿐이다. 마지막으로, 정삼각형 내부의 수의 합이 $3$인 경우는 첫 줄과 둘째 줄로 이루어지는 $1, 1, 1$로 이루어지는 삼각형 하나와, 네 번째 줄의 $3$ 하나로 이루어지는 정삼각형 둘, 모두 세 가지 경우가 있다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설