영역 나누기

원주 위에 $2N$ 개의 점들이 놓여 있다. 각 점에는 $1$ 이상 $N$ 이하의 번호가 붙어 있고, 같은 번호가 붙은 점은 정확히 두 개 있다. 같은 번호가 붙은 점끼리 직선으로 이으면, 원 내부의 영역이 이 직선에 의해 나누어진다.

아래 그림을 보면 $8$ 개의 점이 원주 상에 어떻게 배치되어 있는가에 따라 나누어진 원 내부 영역의 개수가 달라진다. 왼쪽 그림에서는 원 내부가 $7$ 개의 영역으로 나누어진 반면, 오른쪽 그림에선 $11$ 개의 영역으로 나누어졌다. 넓이가 $0$인 영역은 고려하지 않음에 유의하라.

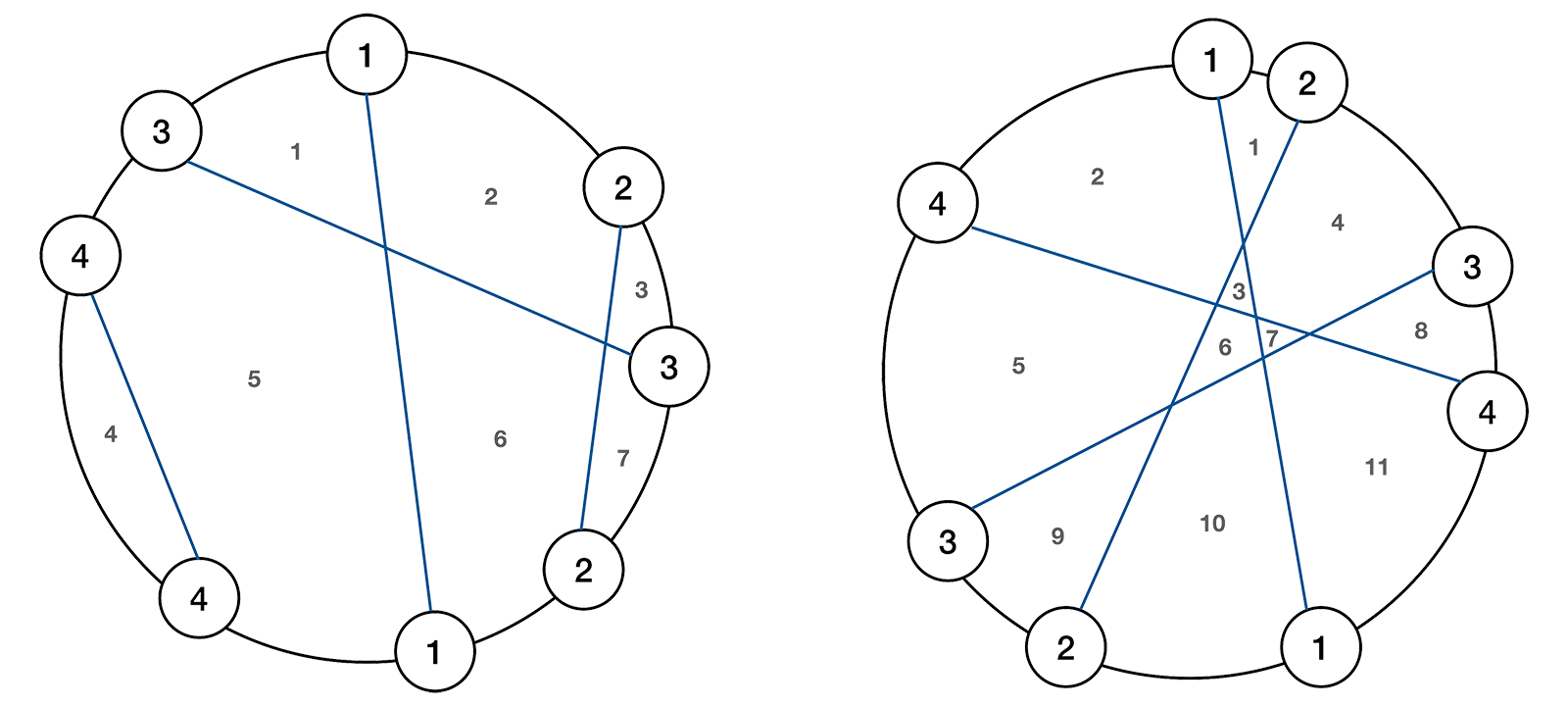
이처럼 원주 상에 배치된 $2N$ 개의 점에 대한 정보가 주어질 때, 위에서 설명한 방법에 따라 그은 직선들에 의해 원 내부의 영역이 최대 몇 개로 나누어 지는지를 구하라.

입력 형식

첫 줄에 정수 $N$이 주어진다. ($1 \le N \le 500\,000$)

이는 원주 위에 점 $2N$ 개가 있다는 뜻이다.

둘째 줄에 $2N$ 개의 정수가 공백으로 구분되어 주어진다. 이 수들은 $1$ 이상 $N$ 이하이며, 하나의 수는 정확하게 두 번 나타난다. 이는 원주 위의 한 점부터 시작해서, 시계 방향으로 원주 위의 점들의 정보를 읽은 것이다. 점들의 위치는 상대적이고, 순서를 지키는 한 자유롭게 정할 수 있음에 유의하라.

출력 형식

첫 줄에 주어진 점들의 정보로 원 내부의 영역을 최대로 나눌 수 있는 개수를 출력한다.

예제

2
2 2 1 1

3

예제 설명

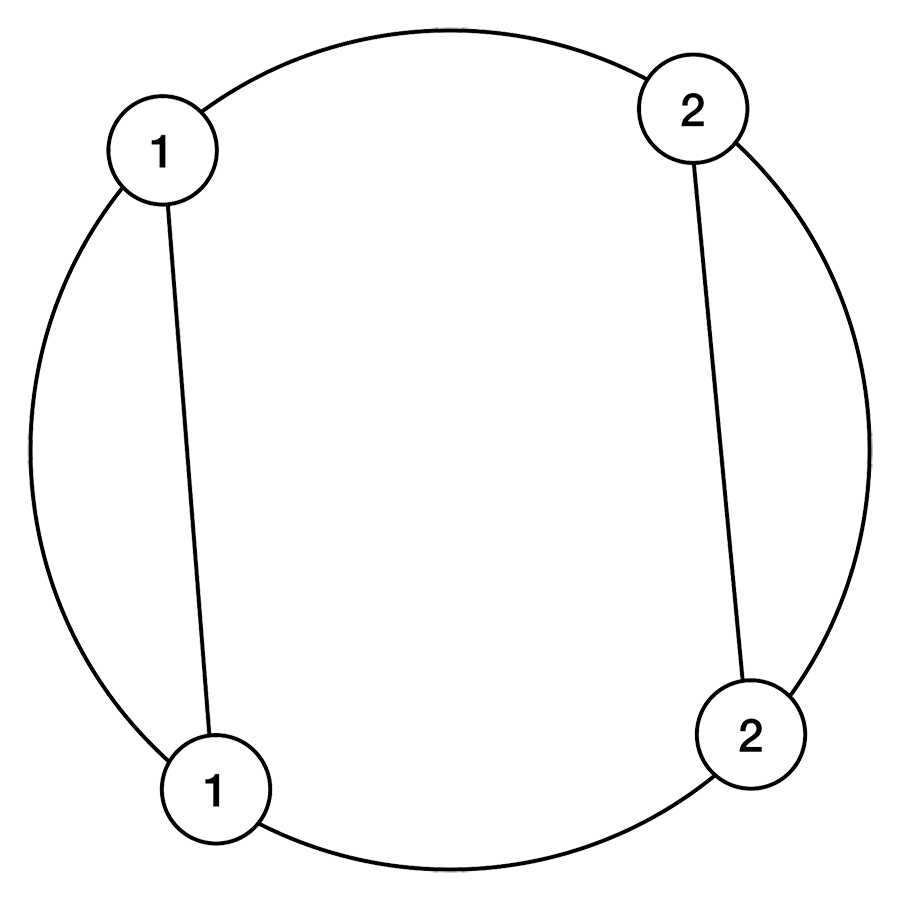
위 예제는 원 위의 한 점 $2$에서 시작해서, 시계 방향으로 이동하면서 가장 먼저 만나는 점이 $2$라는 뜻이다. $1$이 쓰여진 점 둘은 모두 $2$를 잇는 직선에 대해서 같은 방향에 있기 때문에, $1$을 이은 직선은 $2$를 이은 직선과 교차하지 않는다. 따라서 두 직선에 의해서 원은 세 부분으로 나누어진다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞추어야 그 종류에 배정된 점수를 받을 수 있다.

해설