삼각

철수가 사는 동네에는 $N$ 개의 공원이 있고, 각각 두 개의 서로 다른 공원을 양방향으로 연결하는 길들이 $M$ 개 있다. 각 길의 길이를 알고 있다고 하자. 공원들은 $1$부터 $N$까지 번호가 붙어 있다.

철수는 현재 공원 $S$에 있다. 철수는 서로 다른 두 개의 공원 $A$와 공원 $B$를 정해서 공원 $S$에서 공원 $A$로, 공원 $A$에서 공원 $B$로, 다시 공원 $B$에서 공원 $S$로 돌아오려고 한다. 모든 과정에서 전체 이동 거리가 가장 작도록 이동한다. 단, $A$와 $S$는 서로 같지 않고, $B$와 $S$도 서로 같지 않다.

위의 과정에서 같은 공원을 여러 번 지나는 것은 허용되지만, 중간에 공원 $S$를 지나는 것은 허용되지 않는다.

가능한 $A$와 $B$를 정하는 모든 방법에 대해서 전체 이동 거리가 가장 짧은 것을 찾아 그 길이를 출력하는 프로그램을 작성하시오.

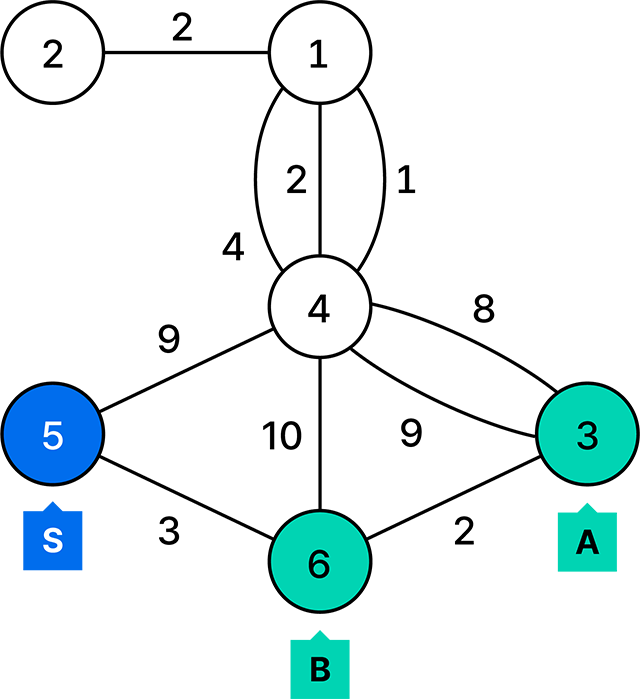
아래 그림은 입력 예제의 경우를 보여 준다. $A = 3$, $B = 6$으로 정하면 총 $10$의 거리를 이동하여 위의 조건을 만족할 수 있다.

입력 형식

첫 줄에 공원의 수와 길의 수, 현재 공원의 번호를 나타내는 세 정수 $N$, $M$, $S$가 공백으로 구분되어 주어진다. ($3 \le N \le 100\,000;$ $3 \le M \le 200\,000;$ $1 \le S \le N$)

이어지는 $M$ 개의 줄의 각 줄에 길의 정보를 나타내는 세 정수 $a$, $b$, $c$가 공백으로 구분되어 주어진다. ($1 \le a, b \le N;$ $1 \le c \le 1\,000\,000\,000;$ $a \ne b$)

이는 공원 $a$와 공원 $b$ 사이를 양방향으로 연결하는 길이 $c$인 길이 존재함을 의미한다.

답이 불가능한 경우는 입력으로 주어지지 않는다.

출력 형식

첫 줄에 답이 되는 정수를 출력한다.

예제

6 10 5
1 4 2
2 1 2
4 6 10
1 4 4
4 3 8
4 5 9
3 4 9
5 6 3
3 6 2
1 4 1

10

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설