적절한 점

평면 위의 임의의 두 점 $p = (x_p, y_p)$와 $q=(x_q, y_q)$에 대해서, $x_p \ge x_q$이고 $y_p \ge y_q$이면, 점 $p$가 점 $q$에 대해 "우세하다"고 표현하기로 한다.

입력으로 $K$ 개의 점 집합 $P_1, P_2, \ldots, P_K$가 주어진다. 각 점 집합에 포함된 점의 개수는 $N_1, N_2, \ldots, N_K$이다. 즉, $N_i = |P_i|$이다. 또, $K$ 개의 음이 아닌 정수 $C_1, C_2, \ldots, C_K$가 주어진다.

이때, 평면 위의 임의의 점 $p$가 아래의 조건을 만족하면, "적절하다"고 말하기로 한다.

• $1\le i \le K$인 각 정수 $i$에 대하여, $p$는 $P_i$에 속한 점들 중에서 정확하게 $C_i$ 개의 점에 대해 우세하다.

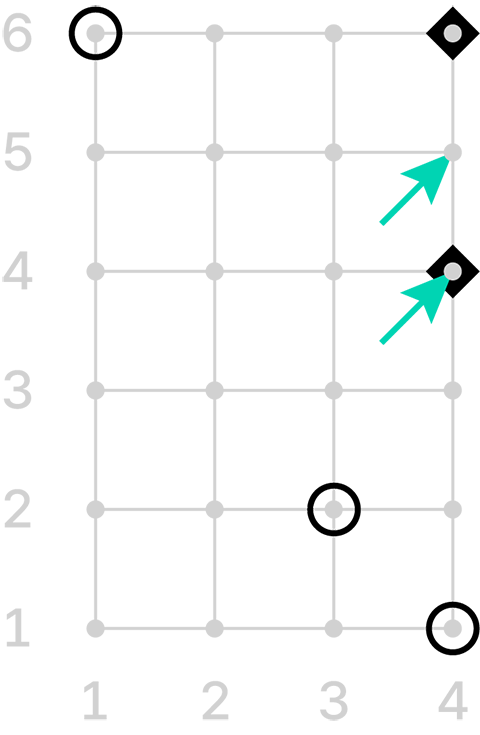
아래 그림은 입력 예제 1의 상황을 나타낸다. 화살표로 표시된 두 개의 점이 적절한 점이다.

$x$ 좌표가 $1$ 이상 $X$ 이하인 정수이고 $y$ 좌표가 $1$ 이상 $Y$ 이하인 정수인 격자점 중에서 적절한 점의 수를 구하는 프로그램을 작성하시오.

입력으로 주어지는 점 집합 $P_1, P_2, \ldots, P_K$에 포함된 점들은 모두 다르다. 또, 거기에 포함된 점들의 $x$ 좌표는 $1$ 이상 $X$ 이하인 정수이고 $y$ 좌표는 $1$ 이상 $Y$ 이하인 정수이다.

입력 형식

첫 줄에 세 정수 $X$, $Y$, $K$가 공백으로 구분되어 주어진다. ($1\le X, Y \le 1\,000\,000\,000;$ $1 \le K \le 500\,000$)

이후 점 집합 $P_1, P_2, \ldots, P_K$가 순서대로 주어진다.

각 점 집합 $P_i$에 대한 입력은 다음과 같다. 첫 줄에 정수 $N_i$가 주어진다. ($1 \le N_i \le 500\,000;$ $K \le \sum_{i=1}^K N_i \le 500\,000$)

이후 이어지는 $N_i$ 개의 각 줄에 $P_i$에 속한 점의 좌표를 나타내는 두 개의 정수 $x$, $y$가 공백으로 구분되어 주어진다. ($1\le x \le X;$ $1\le y \le Y$)

마지막 줄에 $K$ 개의 정수가 주어지며, $C_1, C_2, \ldots, C_K$을 의미한다. ($0 \le C_i \le N_i$)

출력 형식

첫 줄에 문제에서 요구하는 적절한 점들의 개수를 나타내는 정수를 출력한다.

예제 1

4 6 2
2
4 4
4 6
3
3 2
4 1
1 6
1 2

2

예제 2

4 6 2
2
4 4
4 6
3
3 2
4 1
1 6
0 0

11

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설