지름길

아름다운 자연경관 사이를 거닐 수 있도록 산책로가 조성된 호야 공원은 관광객들에게 매우 인기 있는 휴양지이다. 공원 내에는 $N$ 개의 지점이 있고, 각 지점에는 사람들이 휴식을 취할 수 있는 통나무 집이 한 채씩 있으며, 산책로는 이런 지점들 사이를 연결하는 경로로 조성되어 있다. 각 지점은 $1$부터 $N$까지의 번호로 구분된다.

공원 측에선 금년에 관광객을 상대로 흥미로운 미션을 수행하면서 산책할 수 있는 행사를 진행한다.

한번 행사에 참여할 수 있는 최대 인원수는 $N$(공원 내의 지점 수와 같음)이다. 편의상 행사에 참여하는 각 참가자 역시 $1$부터 $N$ 사이의 번호로 구분한다. 행사 시작 전에 각 참가자에겐 동일한 산책로 지도를 준다.

산책로 지도에는 $N$ 개의 지점들이 어떤 산책로로 연결되어 있는지, 그리고 두 지점을 잇는 산책로의 거리가 얼마인지를 나타내는 정보가 들어 있다. 아래 그림은 $6$ 개의 지점을 연결하는 산책로 상황을 예로 보여 준다. 두 지점을 잇는 선분에 적힌 수는 두 지점 사이에 있는 산책로의 거리를 나타낸다. 또한, 지점 6은 행사의 출발지이고 지점 3은 행사의 도착지임을 나타낸다.

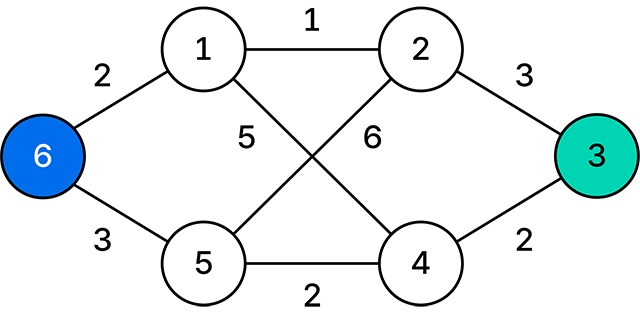
행사에 참여하는 각 사람에겐 서로 다른 미션이 부여되는데, 각 사람이 수행해야 하는 미션이 적힌 쪽지(이를 '미션 쪽지'라 부름)는 $N$ 개의 지점에 흩어져 있다. 정확히 말해 $N$ 개의 각 지점에 있는 통나무 집 안에 미션 쪽지가 하나씩 있다.

행사에 참여하는 각 사람은 아래의 규칙에 따라 산책로를 이동하여야 한다.

• 공원 측에서 지정한 출발지에서 산책을 시작하여야 하고, 또한 공원 측에서 지정한 도착지에 도착하여야 한다.
• 번호가 $i$인 사람은 지점 $i$에 위치한 통나무 집에 있는 미션 쪽지를 읽어야 한다.
• 출발지에서 지점 $i$까지 가는 경로는 최단 경로(지름길)를 따라가야 한다.
• 자기의 미션 쪽지를 읽은 사람은 최단 경로를 따라 도착지로 가야 한다.

대회 직전에 큰 비가 내려 모든 산책로가 통행이 불가능하게 되었다. 공원 측에서는 최소 개수의 산책로를 청소하여 대회를 진행하려고 한다. 단, $N$ 명 중 어떤 사람에 대해서도 이동하는 거리가 늘어나면 안된다.

산책로 지도가 주어질 때, 청소해야 하는 산책로가 몇 개인지, 그리고 어떤 산책로를 청소해야 하는지 찾는 프로그램을 작성하시오.

입력 형식

첫 줄에 지점의 수를 나타내는 정수 $N$, 지점을 잇는 산책로의 개수를 나타내는 정수 $M$, 출발지 $S$와 도착지 $T$가 공백으로 구분되어 주어진다. ($2 \le N \le 100\,000; N - 1 \le M \le 300\,000; 1 \le S, T \le N$)

이어지는 $M$ 개의 줄에 걸쳐, $i$ 번째 줄에는 세 정수 $U_i$, $V_i$, $D_i$가 공백으로 구분되어 주어진다. ($1 \le U_i \le N;$ $1 \le V_i \le N;$ $U_i \ne V_i;$ $1 \le D_{i} \le 1\,000\,000\,000$) 이는 번호가 $i$인 산책로가 지점 $U_i$와 지점 $V_i$를 연결하는 길이 $D_i$인 산책로임을 의미한다. 같은 두 지점 쌍을 연결하는 두 산책로는 존재하지 않는다.

출력 형식

첫 줄에 청소할 산책로의 개수 $K$를 출력한다.

두 번째 줄에 청소할 $K$ 개의 산책로의 번호를 공백으로 구분해 출력한다. 출력하는 정수는 $1$ 이상 $M$ 이하의 서로 다른 정수여야 한다.

만약, 답이 여러 가지인 경우 그중 아무거나 하나 출력한다.

예제 1

6 8 6 3
1 2 1
1 4 5
2 3 3
2 5 6
3 4 2
4 5 2
5 6 3
6 1 2

6
1 3 5 6 7 8

예제 2

4 4 3 4
1 2 1
1 3 1
4 1 3
4 2 1

3
1 2 4

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다. 만약 청소할 산책로의 개수 $K$를 정확하게 구했다면 배정된 점수의 60%를 받을 수 있다. 단, 이 경우에도 서로 다른 $K$ 개의 산책로 번호를 출력해야 한다.

해설