물풍선 애널리스트

물풍선 아티스트 마리드를 기억하는가? 마리드는 다음 작품을 위해 총 $N$ 개의 물풍선을 2차원 격자판에 설치했다. 이때 $i$ 번째 물풍선은 $(x_i, y_i)$ 칸에 세기 $p_i$로 설치되어 있다. 설치된 물풍선의 위치는 모두 다르다.

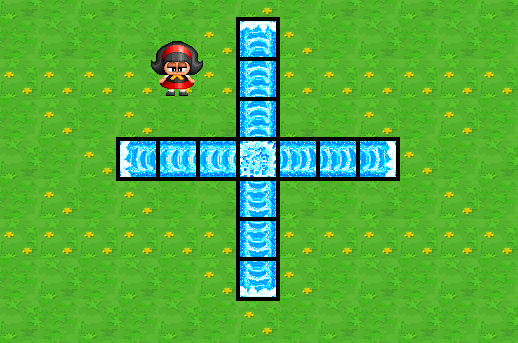
물풍선이 터지면 물풍선의 세기만큼 십자모양으로 물줄기를 발사한다. 다시 말해, 가로 방향으로는 $(x_i - p_i, y_i)$, $(x_i - p_i + 1, y_i)$, $\cdots$, $(x_i + p_i - 1, y_i)$, $(x_i + p_i, y_i)$에 해당하는 칸에 물줄기가 닿게 되며, 세로방향으로는 $(x_i, y_i - p_i)$, $(x_i, y_i - p_i + 1)$, $\cdots$, $(x_i, y_i + p_i - 1)$, $(x_i, y_i + p_i)$에 해당하는 칸에 물줄기가 닿게 된다. 물론, $(x_i, y_i)$에도 물줄기가 닿게 된다. 만약 이 물줄기가 다른 물풍선이 있는 칸에 닿는다면 그 물풍선 또한 터지며, 이로 인해 연쇄적인 물풍선 폭발이 일어날 수도 있다. 단, 각각의 물줄기가 닿는 범위는 독립적이며 그 과정에서 터지는 다른 물폭탄의 영향을 받지 않는다. 즉, 물풍선이 중첩된다고 세기가 커지는 것은 아니다.

그런데 이때 문제가 발생했다. 설치된 물풍선들의 세기 $p_i$를 모두 잊어버린 것이다! 마리드는 물풍선 애널리스트 모스에게 의뢰해서 다음과 같은 정보를 얻었다.

• $i$ 번째 물풍선을 터트렸을 때 $N$ 개의 물풍선이 모두 터지는지 여부 $t_i$ ($0 \le t_i \le 1$)
  • $t_i$가 $1$이면 $N$ 개의 물풍선이 모두 터진다는 뜻이고, $t_i$가 $0$이면 그렇지 않다는 뜻이다.

모스는 유능한 물풍선 애널리스트이기 때문에, 모스의 정보가 틀렸을 가능성은 없다. 다시 말해, $t_i$를 모두 만족하는 물풍선 세기 $p_i$의 조합의 존재함이 보장된다.

설치되어 있는 $N$ 개의 물풍선 위치와 모스의 정보가 주어질 때, 이를 만족하는 물풍선 세기의 조합을 구하는 프로그램을 작성하시오.

입력 형식

첫 줄에 설치된 물풍선의 수를 나타내는 정수 $N$이 주어진다. ($1 \le N \le 500\,000$)

이어지는 $N$ 줄의 $i$ 번째 줄에 $i$ 번째 물풍선의 위치와 모스의 정보를 나타내는 정수 $x_i$, $y_i$, $t_i$가 공백으로 구분되어 주어진다. ($1 \le x_i,y_i \le 1\,000\,000\,000$; $0 \le t_i \le 1$)

주어지는 물풍선의 위치는 서로 다르다.

출력 형식

$i$ 번째 줄에 $i$ 번째 물풍선의 세기를 나타내는 $p_i$를 출력한다. ($1 \le p_i \le 1\,000\,000\,000$)

주어진 $t_i$를 모두 만족하며, 출력 형식 또한 만족하는 $p_i$의 조합의 존재함이 보장된다. 만약 답이 여러 가지인 경우, 그중 아무거나 하나 출력한다.

예제

4
1 1 1
5 1 0
5 3 0
1 3 1

4
2
2
2

예제 설명

입력 예제의 경우 주어진 출력 예제 외에도 가능한 올바른 출력들이 더 존재할 수 있으며, 그 중 어느 것을 출력해도 된다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설