이차원 평면에 축과 평행한 선분, 즉, 수평선분이 개 놓여있다. 번째 선분의 양 끝점은 와 이다.
또한, 레이저 발사기 개가 있다. 편의상 레이저 발사기에 번부터 번까지 번호가 매겨져 있다. 번 레이저 발사기는 에 놓여 있다. 번 레이저 발사기에서 발사된 레이저는 축에 평행하게 좌표가 증가하는 수직 방향으로 뻗어나가며, 개의 선분을 뚫고 지나갈 수 있다. 번 레이저 발사기에서 발사된 레이저가 선분을 번 뚫고 지나간 이후 선분을 만나면 더 이상 뻗어나가지 않고 그 자리에서 소멸한다. 레이저가 뚫고 지나간 선분은 그 즉시 파괴되어 없어진다.
레이저 발사기가 번호 순서대로 레이저를 발사할 때, 각 레이저가 뻗어나간 거리를 구하는 프로그램을 작성하라. 어떤 레이저는 무한히 뻗어나갈 수 있음에 유의하라.
입력 형식
첫 줄에 수평선분의 개수를 나타내는 정수 과 레이저 발사기의 개수를 나타내는 정수 이 공백으로 구분되어 주어진다. ()
이어지는 개의 줄의 번째 줄에는 번째 선분의 정보를 나타내는 세 정수 , , 가 공백으로 구분되어 주어진다. (; )
이어지는 개의 줄의 번째 줄에는 번 레이저 발사기의 정보를 나타내는 세 정수 , , 가 공백으로 구분되어 주어진다. (; )
주어지는 모든 좌표는 서로 다르고, 주어지는 모든 좌표도 서로 다르다.
출력 형식
개의 줄에 걸쳐 답을 출력한다.
번째 줄에 번 레이저 발사기에서 발사된 레이저가
뻗어나간 거리를 출력한다.
만약, 레이저가 무한히 뻗어나가면 -1을 출력한다.
예제
입력
5 3 4 11 7 8 12 8 6 13 3 1 7 4 2 10 9 5 2 2 9 5 2 3 6 1
출력
7 -1 -1
예제 설명
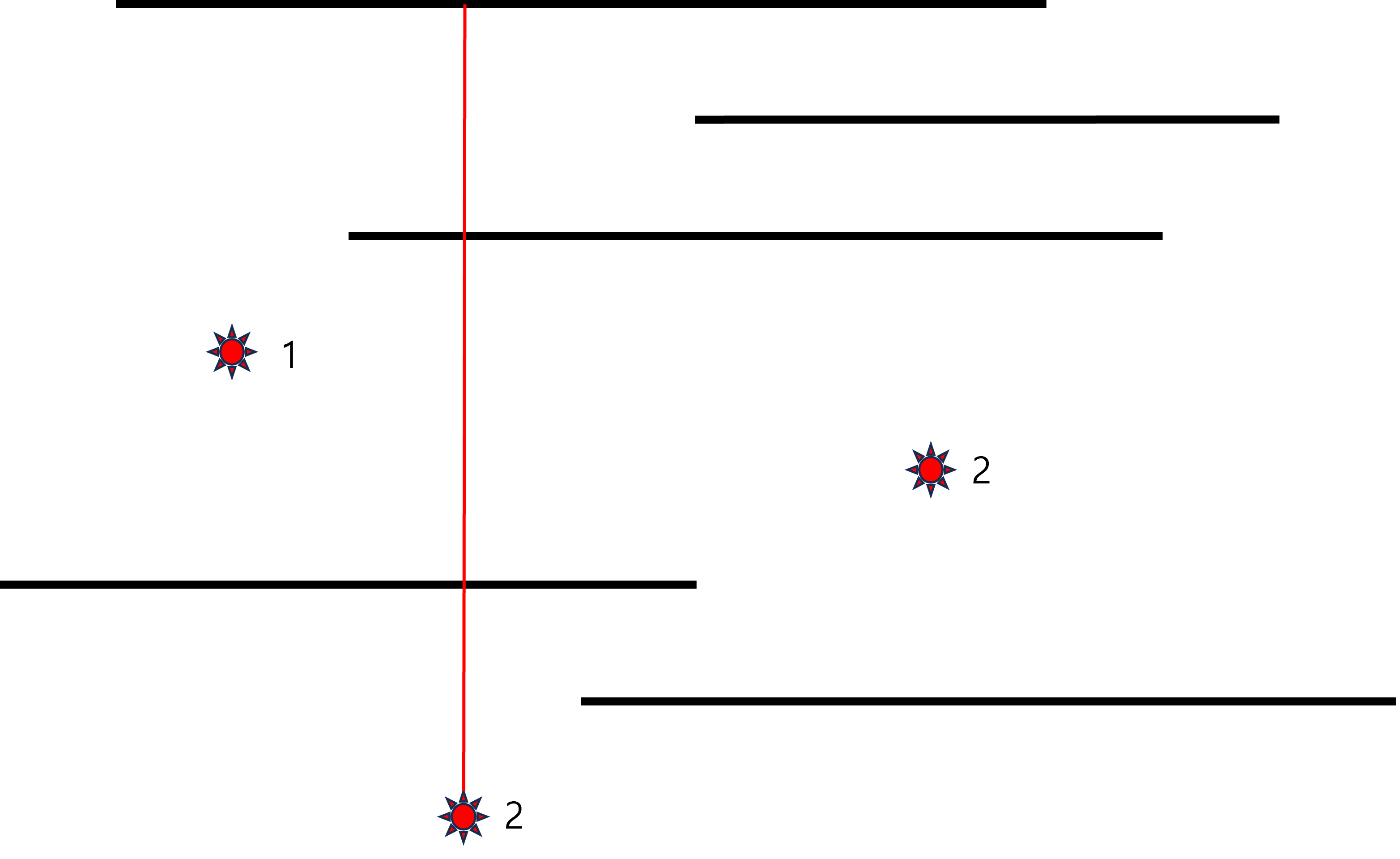
번 레이저 발사기에서 레이저가 발사된 이후의 순간이다. 이 레이저는 선분 개를 뚫고 지나갈 수 있다.
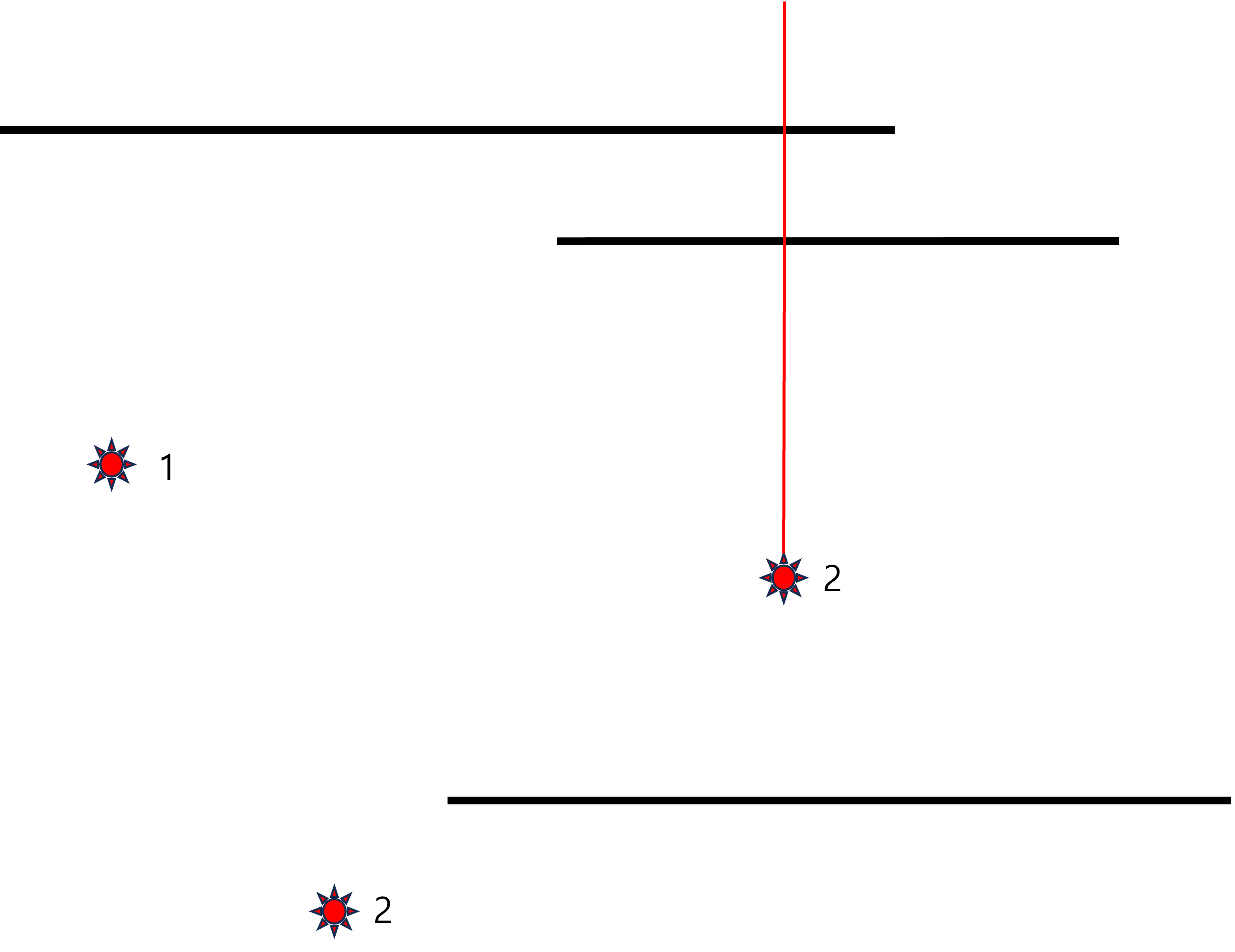
처음 발사된 레이저에 의해 선분 개가 파괴되어 없어지고, 번 레이저 발사기에서 레이저가 발사된 이후의 순간이다. 이 레이저는 선분 개를 뚫고 지나갈 수 있으며, 이후 무한히 뻗어나간다.

번 레이저 발사기에서 레이저가 발사된 이후의 순간이다. 이 레이저는 선분 개를 뚫고 지나갈 수 있으며, 이후 무한히 뻗어나간다.
채점 방식
입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.
종류 1: 21점
종류 2: 22점
임의의 실수 에 대해, 직선 와 만나는 선분은 개보다 많지 않다.
종류 3: 23점
종류 4: 23점
;
종류 5: 11점
추가적인 제한 조건이 없음.