오솔길

이차원 평면에 $N$ 개의 점이 주어진다. 점들의 $x$ 좌표는 서로 다르고, $y$ 좌표도 서로 다르다.

점들이 전체적으로 왼쪽 아래에서 오른쪽 위로 올라가는 모양이면 이 모양을 오솔길이라고 부른다. 구체적으로, 모든 가능한 점들의 쌍에 대해 $x$ 좌표가 더 큰 점이 $y$ 좌표도 더 큰 경우를 오솔길이라고 부른다.

주어진 점들의 집합을 오솔길로 만들려고 한다. 이를 위해 할 수 있는 작업은 임의의 두 개의 점을 골라서 $x$ 좌표를 교환하는 것이다. 즉, 작업 전의 두 점의 좌표가 각각 $(x_1, y_1)$, $(x_2, y_2)$이었으면 작업 후에 좌표는 각각 $(x_2, y_1)$, $(x_1, y_2)$가 된다.

주어진 점들을 오솔길로 만들기 위해 필요한 최소 작업의 수를 구하는 프로그램을 작성하시오.

입력 형식

첫 줄에 점의 개수 $N$이 주어진다. ($1 \le N \le 200\,000$)

이어지는 $N$ 개의 줄의 $i$ 번째 줄에는 $i$ 번째 점의 좌표 $(x_i, y_i)$에 해당하는 두 정수 $x_{i}$와 $y_{i}$가 공백으로 구분되어 주어진다. ($1 \le x_{i}, y_{i} \le 1\,000\,000\,000$)

$x_{i}$는 모두 다르고, $y_{i}$도 모두 다르다. 즉, $i \ne j$인 모든 $i$, $j$에 대해서 $x_i \neq x_j$이고 $y_i \neq y_j$이다.

출력 형식

첫 줄에 주어진 점들을 오솔길로 만들기 위해 필요한 최소 작업의 수를 출력한다.

예제

5
1 1
2 3
3 4
4 2
5 5

2

예제 설명

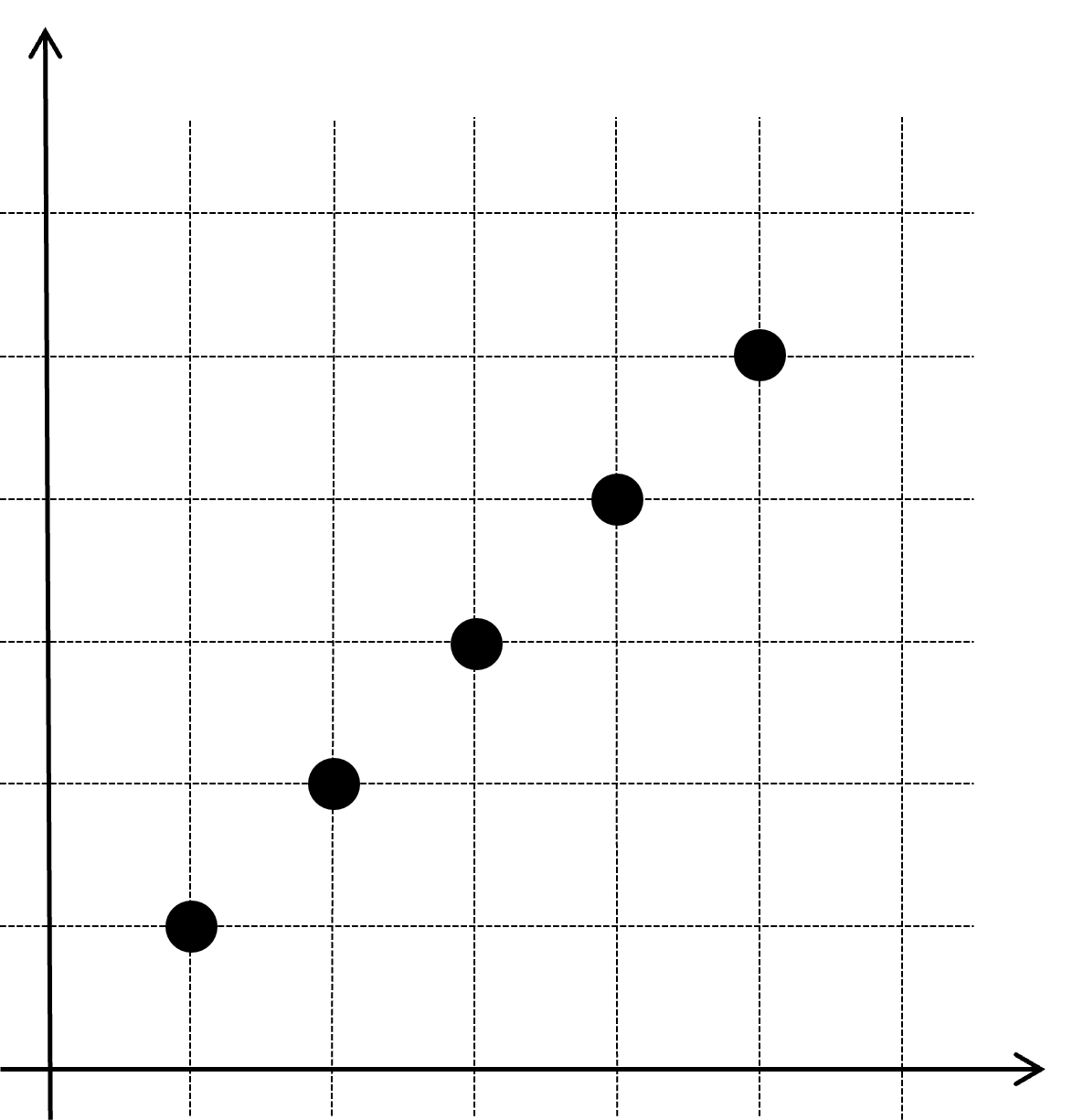
주어진 점들을 좌표 평면에 표현하면 아래와 같다. 아래 그림에서 화살표로 표시된 두 점의 $x$ 좌표를 교환하면 그 아래 그림과 같이 된다.

위 그림에서 다시 화살표로 표시된 두 점의 $x$ 좌표를 교환하면 아래 그림과 같이 되어 오솔길이 된다. 이 경우가 가장 작은 횟수의 작업을 하는 방법들 중 하나이다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설