편지

$N$ 개의 정점으로 이루어진 트리가 있다. 트리의 정점들은 $1$번부터 $N$번까지 번호가 붙어 있다. 트리의 루트는 $1$번 정점이고, $i$번 정점의 부모는 $P_{i}$번 정점이다. 초기에 $i$번 정점에 $A_{i}$ 개의 편지를 가지고 있다.

매초마다, 하나 이상의 편지를 가지고 있는 모든 루트가 아닌 정점은 자신이 가진 편지 중 하나를 부모 정점으로 보낸다. 또한, 루트 정점은 하나 이상의 편지를 가지고 있을 경우 그 중 하나를 버린다. 어떤 정점이 편지를 부모 정점으로 보내는 것은 부모에 편지가 몇 개 있는지와는 무관하다. 모든 정점은 동시에 편지를 보내기 때문에, 자식 정점으로부터 전달받은 편지가 곧바로 부모 정점으로 전달되지는 않는다.

트리에 편지가 하나도 존재하지 않을 때까지 몇 초가 필요할 지 계산하려고 한다. 단, 처음부터 트리에 편지가 하나도 존재하지 않는 경우는 $0$ 초가 필요한 것으로 생각하자.

또한, 업데이트가 $Q$ 개 주어진다. $i$ 번째 업데이트는 $X_{i}$번 정점에 있는 편지의 개수를 $Y_{i}$ 개로 바꾼다.

여러분의 프로그램은 초기 트리에서 모든 편지가 버려지는 데 몇 초가 필요한지 계산하여야 하며, 각 업데이트 이후의 트리에서 모든 편지가 버려지는 데 몇 초가 필요한지 계산해야 한다. 각 업데이트는 이전 업데이트들이 모두 적용된 트리에 누적하여 적용되는 것임에 유의하라.

편지들을 보내거나 버리는 과정은 실제로 트리에 적용되지 않음에 주의하라. 즉, 모든 편지가 버려지는 데 몇 초가 필요한지는 계산만 하는 것이며 트리의 편지 위치들을 바꾸지는 않는다.

입력 형식

첫 줄에 정점의 수 $N$과 업데이트의 수 $Q$가 공백으로 구분되어 주어진다. ($2 \le N \le 200\,000;$ $0 \le Q \le 200\,000$)

그다음 줄에 $N - 1$ 개의 정수 $P_{2}, \cdots, P_{N}$이 공백으로 구분되어 주어진다. ($1 \le P_{i} < i$)

그다음 줄에 $N$ 개의 정수 $A_{1}, \cdots, A_{N}$이 공백으로 구분되어 주어진다. ($0 \le A_{i} \le 1\,000\,000\,000$)

이어지는 $Q$ 개의 줄의 $i$ 번째 줄에는 두 정수 $X_{i}$와 $Y_{i}$가 공백으로 구분되어 주어진다. ($1 \le X_{i} \le N;$ $0 \le Y_{i} \le 1\,000\,000\,000$)

출력 형식

첫 줄에 초기 트리에 대한 답을 출력한다.

이어지는 $Q$ 개의 줄의 $i$ 번째 줄에 $i$ 번째까지 업데이트가 적용된 이후의 트리에 대한 답을 출력한다.

예제 1

5 1
1 1 1 1
0 0 1 2 0
2 2

4
6

예제 2

6 5
1 2 3 4 5
0 0 0 0 0 0
4 2
6 1
3 2
1 2
1 3

0
5
6
7
7
8

예제 설명

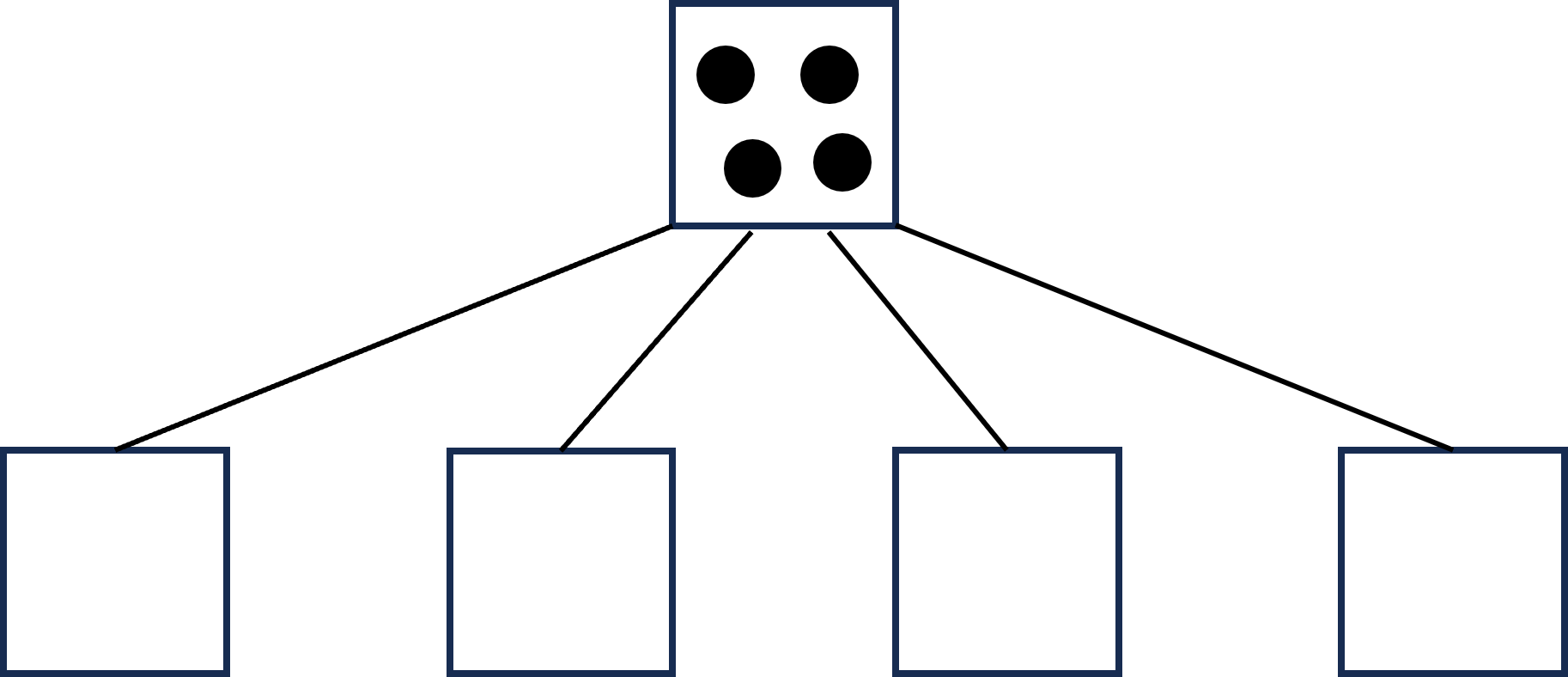
예제 1에서, 초기 트리의 모양과 각 정점에 있는 편지의 개수는 아래 그림과 같다. 그림의 사각형이 정점이며, 사각형 안의 점들이 편지들이다.

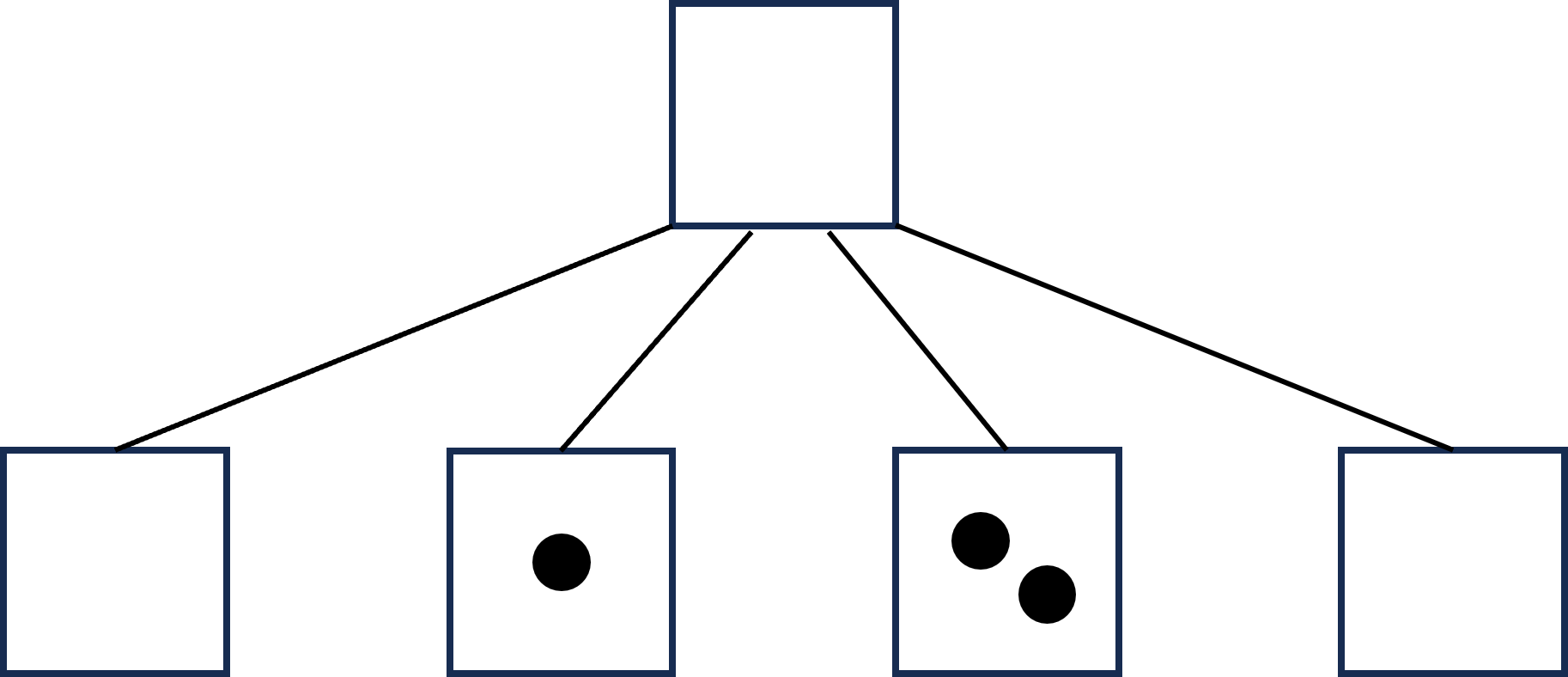
$1$ 초가 지나면 편지들은 아래와 같이 이동한다.

$1$ 초가 더 지나면 루트 정점에서 한 개의 편지가 버려지면서 아래와 같은 상황이 된다.

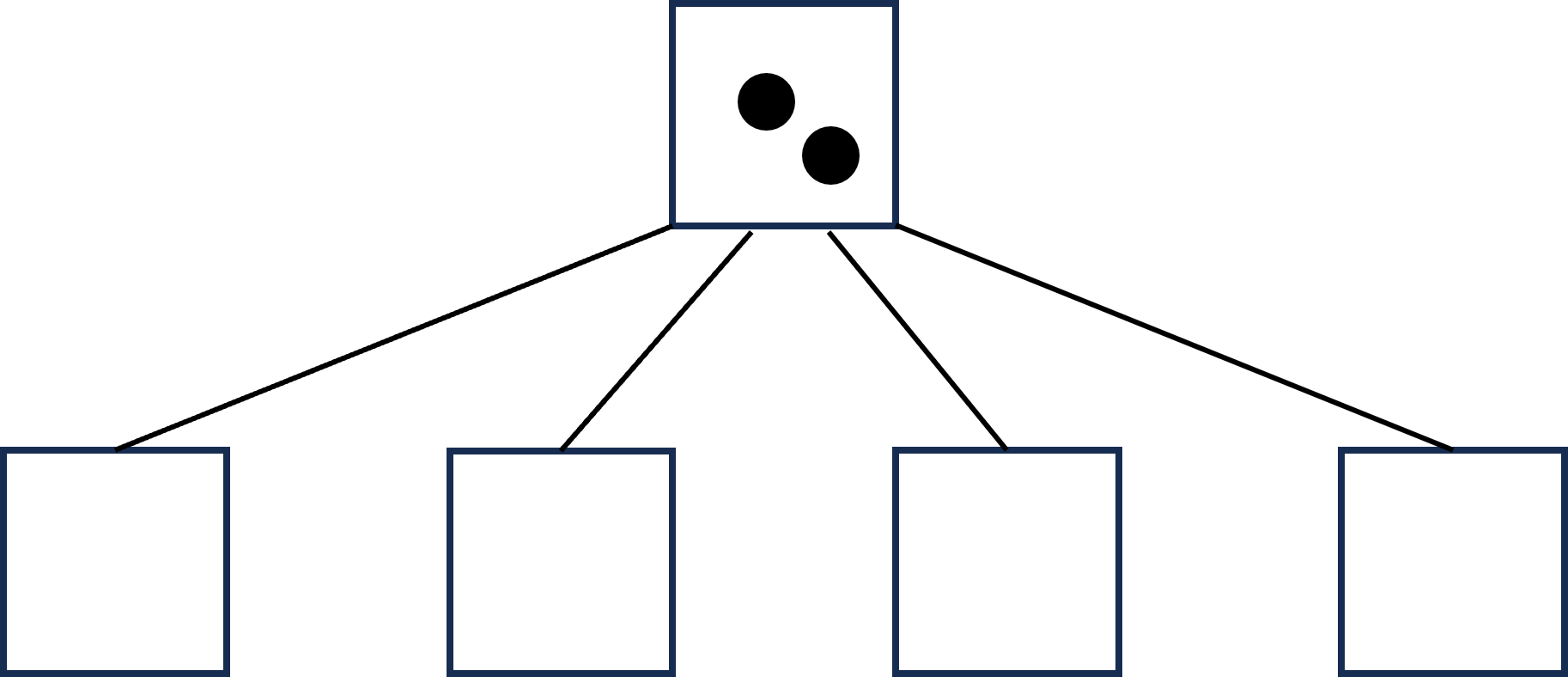
$1$ 초가 더 지나면 루트 정점에 한 개의 편지가 남은 상황이 된다. 따라서, 초기 트리에서 모든 편지가 버려지는데 $4$ 초가 걸린다.

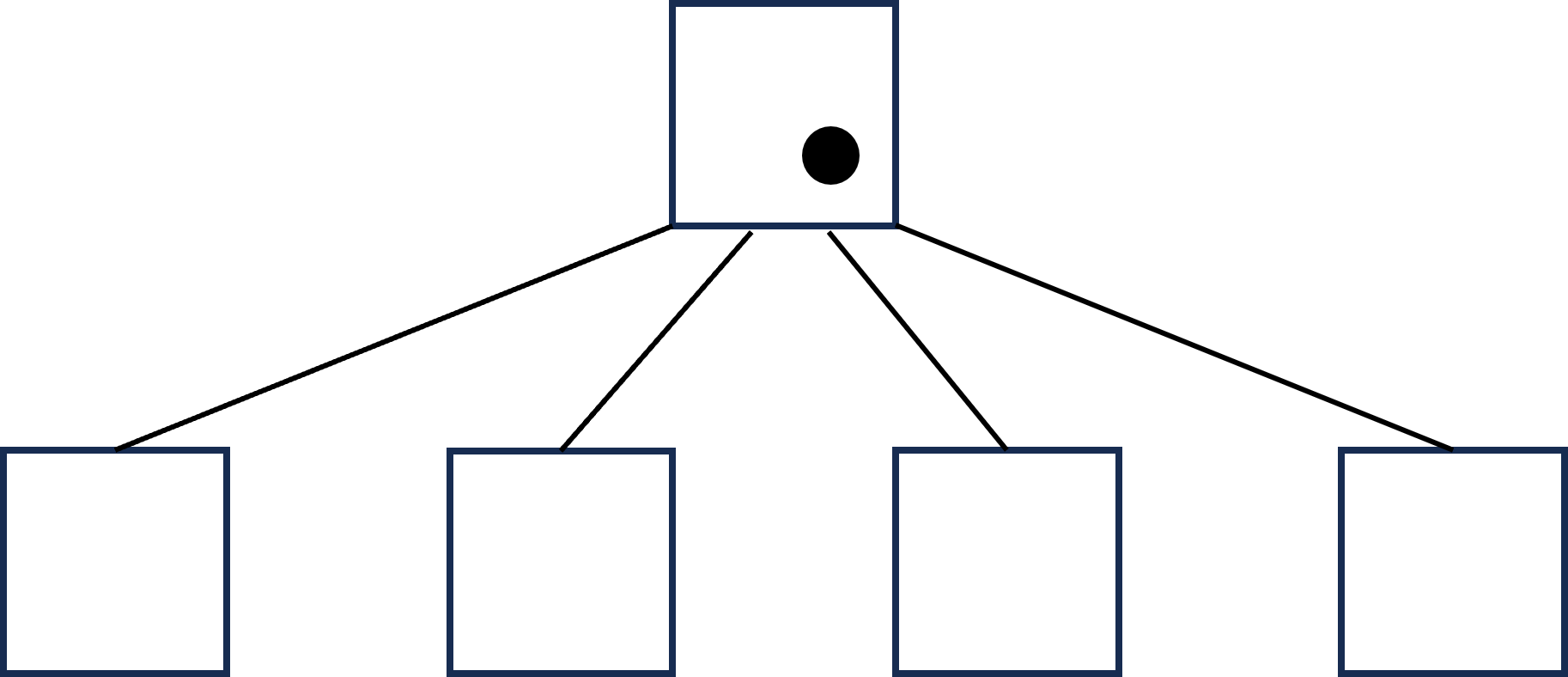
유일한 업데이트가 초기 트리에 적용되고 나면 아래와 같은 상황이 된다.

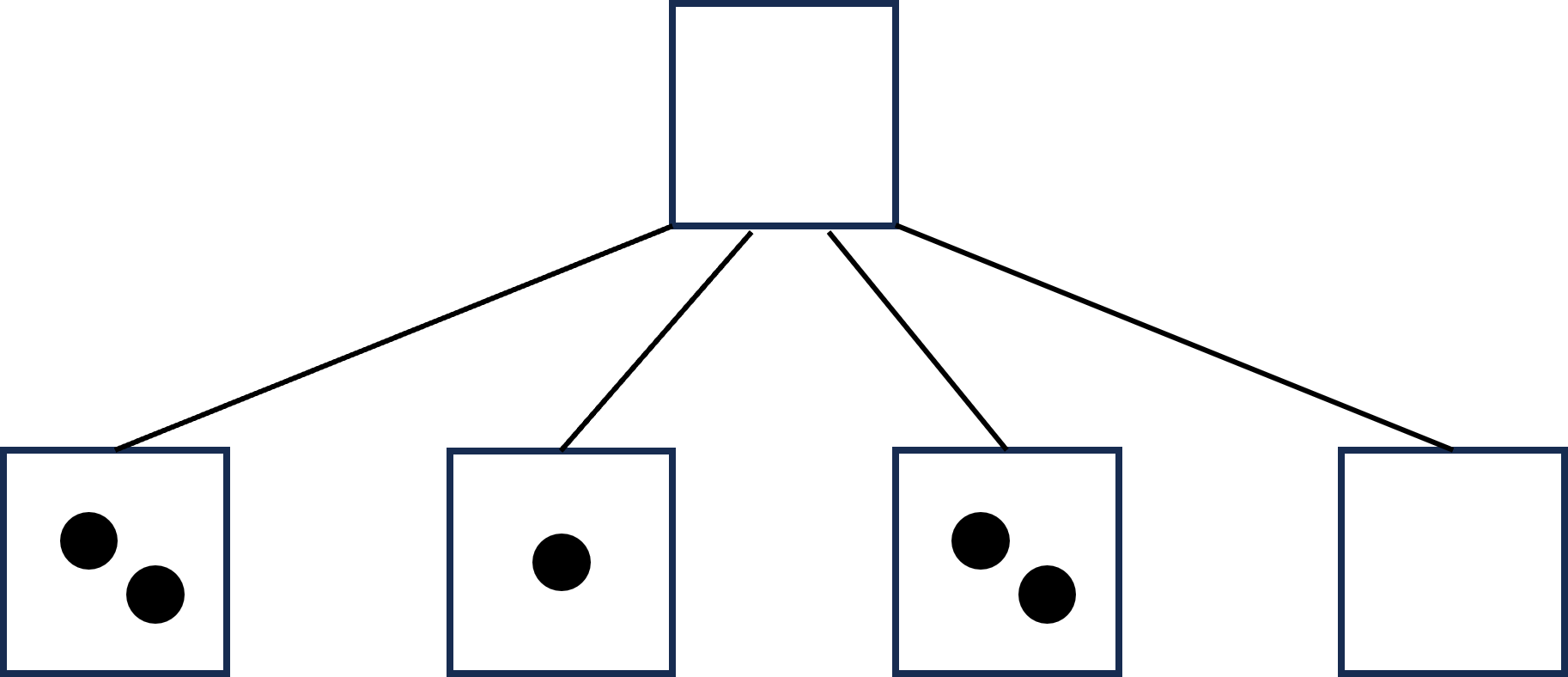
$1$ 초가 지나면 아래와 같은 상황이 된다.

$1$ 초가 더 지나면 루트 정점에만 네 개의 편지가 있는 상황이 된다. 따라서 이 경우에는 $6$ 초가 지난 후 모든 편지가 버려진다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설