크기가 (X+1)×(Y+1) 인 격자가 있다.
이 격자의 맨 왼쪽 아래 격자점의 좌표는 (0,0)이고,
맨 오른쪽 위 격자점의 좌표는 (X,Y)다.
이 격자 위에 별자리 그림이 그려져 있다.
이 별자리 그림은 L 개의 빨간색 선분으로 되어 있고,
각 선분의 양 끝점은 모두 격자점 위에 있다.
별자리 그림과 별개로 N 개의 별이 격자점에 놓여 있고,
이들 중 두 개의 별을 잇는 M 개의 노란색 선분이 있다.
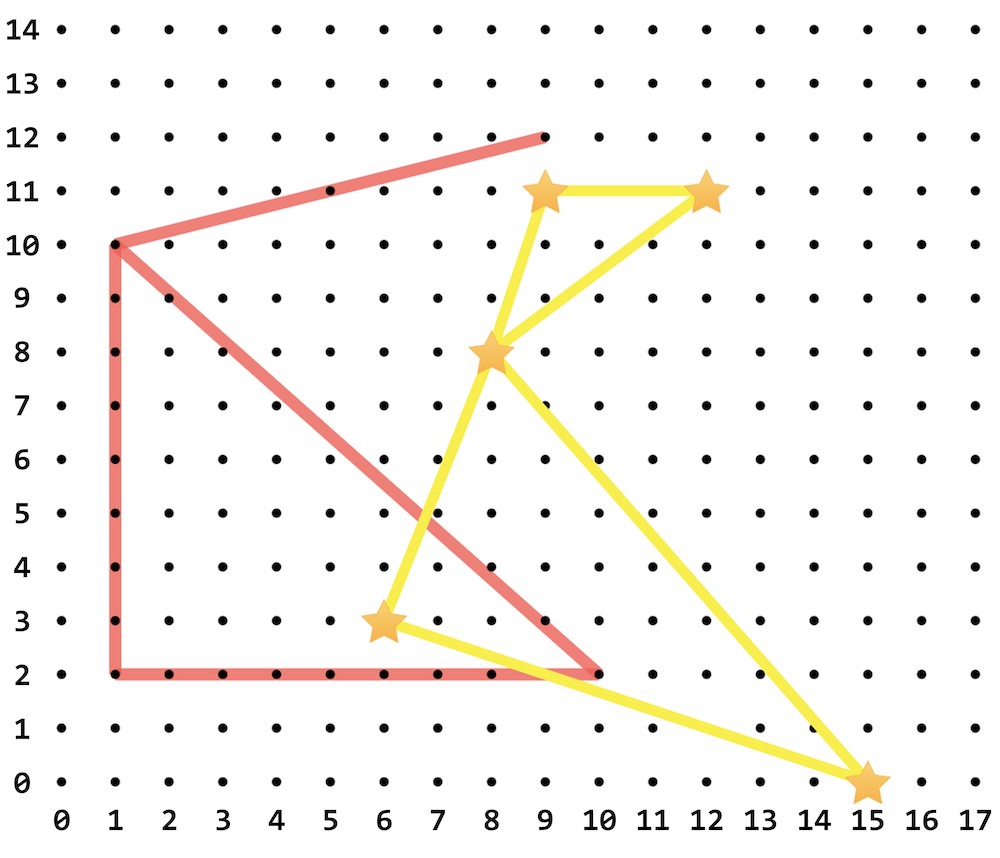
아래의 그림은 X=17, Y=14인 격자에서
4 개의 빨간색 선분으로 구성된 별자리를 보여준다.
또한, 5 개의 별이 격자점에 놓여 있고,
6 개의 노란색 선분이 어느 별이 어떻게 연결되어 있는지를 보여준다.
즉, L=4, N=5, M=6이다.
여러분은 별을 끌어 다른 격자점 위로 움직일 수 있다.
이 과정에서 두 별이 겹치면 안 된다.
노란색 선분의 끝점은 별의 위치를 따라가기 때문에,
별들이 움직이면 노란색 선분도 같이 움직인다.
여러분은 별을 움직여서
별에 연결된 노란색 선분이 만드는 그림이
빨간색 선분으로 그려진 별자리 그림과 일치되도록 해야 한다.
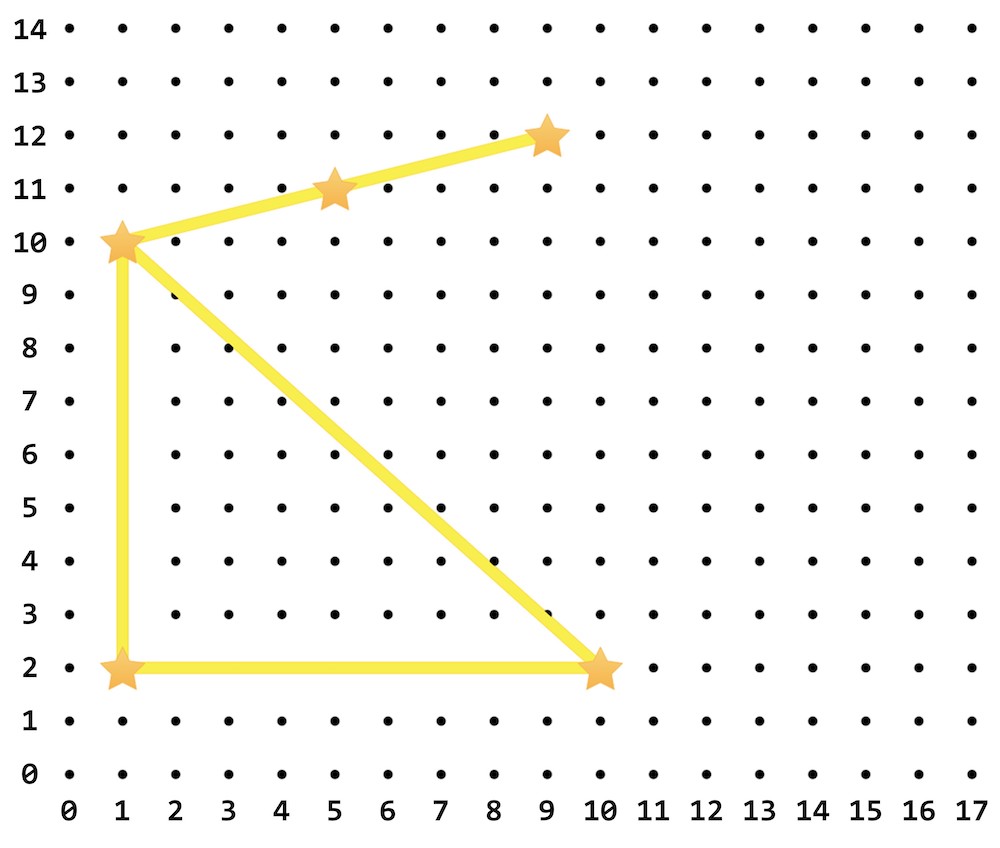
첫 그림의 5 개의 별을 위의 그림처럼 옮기면
노란색 선분이 그리는 그림이
정확하게 별자리 그림과 같아짐을 알 수 있다.
여러분은 가능하면 별이 이동한 거리의 합 R을 가능한 작게 해야 한다.
초기에 (x,y)에 놓여있던 별이 (Δx,Δy)만큼 움직여서
최종 위치가 (x+Δx,y+Δy)라면,
이 별이 이동한 거리는 (Δx×Δx)+(Δy×Δy)이다.
입력 형식
첫 줄에 격자의 크기를 나타내는 두 정수 X와 Y가
공백으로 구분되어 주어진다.
(2≤X,Y≤50)
그다음 줄에 빨간색 선분의 수 L이 주어진다.
(1≤L≤200)
이어지는 L 개의 줄의 i 번째 줄에는
i 번째 빨간색 선분에 대한 정보를 나타내는 네 정수
Ai, Bi, Ci, Di가
공백으로 구분되어 주어진다.
이는 i 번째 빨간색 선분의 양 끝점의 좌표가
(Ai,Bi)와 (Ci,Di)임을 의미한다.
그다음 줄에 별의 수 N이 주어진다. (2≤N≤300)
이어지는 N 개의 줄의 i 번째 줄에는
i 번째 별에 대한 정보를 나타내는 두 정수
Ei와 Fi가
공백으로 구분되어 주어진다.
이는 i 번째 별이 초기에
(Ei,Fi)에 위치함을 의미한다.
(0≤Ei≤X; 0≤Fi≤Y)
그다음 줄에 노란색 선분의 수 M이 주어진다.
(1≤M≤300)
이어지는 M 개의 줄의 i 번째 줄에는
i 번째 연결된 두 별의 정보를 나타내는 두 정수
Gi와 Hi가
공백으로 구분되어 주어진다.
이는 i 번째 노란색 선분에 연결된 두 별의 번호를 의미한다.
(1≤Gi,Hi≤N; Gi=Hi)
출력 형식
N 개의 줄에 답을 출력한다.
i 번째 줄에
i 번째 별이 옮겨진 위치를 나타내는
두 정수 Ei′, Fi′를 공백으로 구분하여 출력한다.
이는 i 번째 별이 (Ei,Fi)에서 (Ei′,Fi′)로
이동했음을 의미한다.
예제
입력
17 14
4
1 2 10 2
1 2 1 10
10 2 1 10
1 10 9 12
5
6 3
8 8
9 11
12 11
15 0
6
1 2
1 5
2 5
2 3
3 4
2 4
출력
1 2
1 10
5 11
9 12
10 2
채점 방식
이 문제는 풀이 소스 코드를 제출하지 않고, 각 테스트 케이스의 입력 데이터를 다운받아 알맞은 출력 파일을 만들어 출력 파일만을 제출하는 문제다.
문제 해결을 도와주는 시뮬레이터가 아래 미션에 대해 제공된다. 제공되는 시뮬레이터는 최신 버전의 크롬 브라우저에서 여는 것을 권장한다.
이 문제의 총점은 모든 미션의 점수의 합으로 계산된다.
각 미션의 점수를 계산하는 방법은 다음과 같다.
- S : 미션의 만점
- P : 미션에 대한 참가자의 점수
- α, β : 미션마다 정해진 상수
- α : 이동 거리 점수에서 만점을 받을 수 있는 총 이동 거리
- β : 이동 거리 점수에서 만점의 1/3을 받을 수 있는 총 이동 거리
먼저, 별자리 점수 Pstar는 다음과 같이 계산된다.
- linput : 주어진 별자리 그림의 길이
- loutput : 참가자가 그린 그림의 길이
- lcommon : 주어진 별자리 그림과 참가자의 그림에서 겹치는 부분의 길이
- Pstar=max{0,40×2×linputlinput−loutput+2×lcommon}
다음으로, 이동 거리 점수 Pmove는 다음과 같이 계산된다.
- R≤α 인 경우: Pmove=30
- α<R≤β 인 경우: Pmove=10+20×(β−αβ−R)2
- R≥β 인 경우: Pmove=10×(β/R)2
이때, 참가자의 점수 P는 이러하다.
- 참가자의 그림이 주어진 별자리 그림과 완벽하게 일치하는 경우: P=S×(Pstar+2×Pmove)/100
- 그렇지 않은 경우: P=S×(Pstar+Pmove)/100
이후, P는 최종적으로 0.1 단위로 버림된다.
단, 참가자의 출력이 올바르지 않은 경우
(출력 형식을 맞추지 않았거나, 제약 조건을 지키지 않는 등)
P=0이다.
각 미션의 정보는 다음과 같다.
| # | X | Y | S | α | β |
|---|
| 1 | 10 | 10 | 6 | 13.300563 | 36 |
| 2 | 18 | 18 | 8 | 164.031821 | 166 |
| 3 | 20 | 9 | 11 | 162.4181685 | 162.6 |
| 4 | 16 | 10 | 13 | 212.769030 | 213.1 |
| 5 | 34 | 27 | 14 | 954.2131126 | 960 |
| 6 | 28 | 25 | 14 | 907.8216973 | 910 |
| 7 | 18 | 16 | 14 | 400.1135114 | 401 |
| 8 | 42 | 16 | 20 | 5862.064672 | 5864 |
미션마다 만점을 받을 수 있는 출력이 존재함이 보장된다.
해설