계단

$N$ 개의 직사각형이 좌우로 붙어 있다. 각 직사각형의 너비는 $1$이다. 왼쪽에서 $i$ 번째 직사각형의 높이는 $A_i$이다.

$1$보다 큰 $K$에 대해, $N$ 개의 직사각형 중 $K$ 개를 선택하여, 원래 순서를 유지하며 이어 붙였을 때 인접한 직사각형의 높이 차이가 모두 동일하면, 계단이라고 부른다.

즉, $s_1 \lt s_2 \lt \cdots \lt s_K$인 어떤 $K$ 개의 직사각형들의 높이가 $A_{s_1}, A_{s_2}, \ldots, A_{s_K}$일 때 $A_{s_1}-A_{s_2}=A_{s_2}-A_{s_3}=\cdots =A_{s_{K-1}}-A_{s_K}$를 만족하는 경우를 말한다. 여기서, $2$ 개의 직사각형의 모임은 항상 계단이 된다는 것에 유의하라.

직사각형들의 높이가 주어졌을 때 계단이 되는 경우의 수를 계산하는 프로그램을 작성하라.

입력 형식

첫 줄에 직사각형의 개수를 나타내는 정수 $N$이 주어진다. ($1 \le N \le 2\,000$)

그다음 줄에 직사각형의 높이를 나타내는 $N$ 개의 정수 $A_1, A_2, \cdots, A_N$이 공백으로 구분되어 주어진다. ($1 \le A_i \le 1\,000\,000\,000$)

출력 형식

첫 줄에 계단이 되는 방법의 수를 $1\,000\,000\,007$로 나눈 나머지를 출력한다.

예제

5
1 1 3 5 4

12

예제 설명

입력 예제는 아래 그림과 같다.

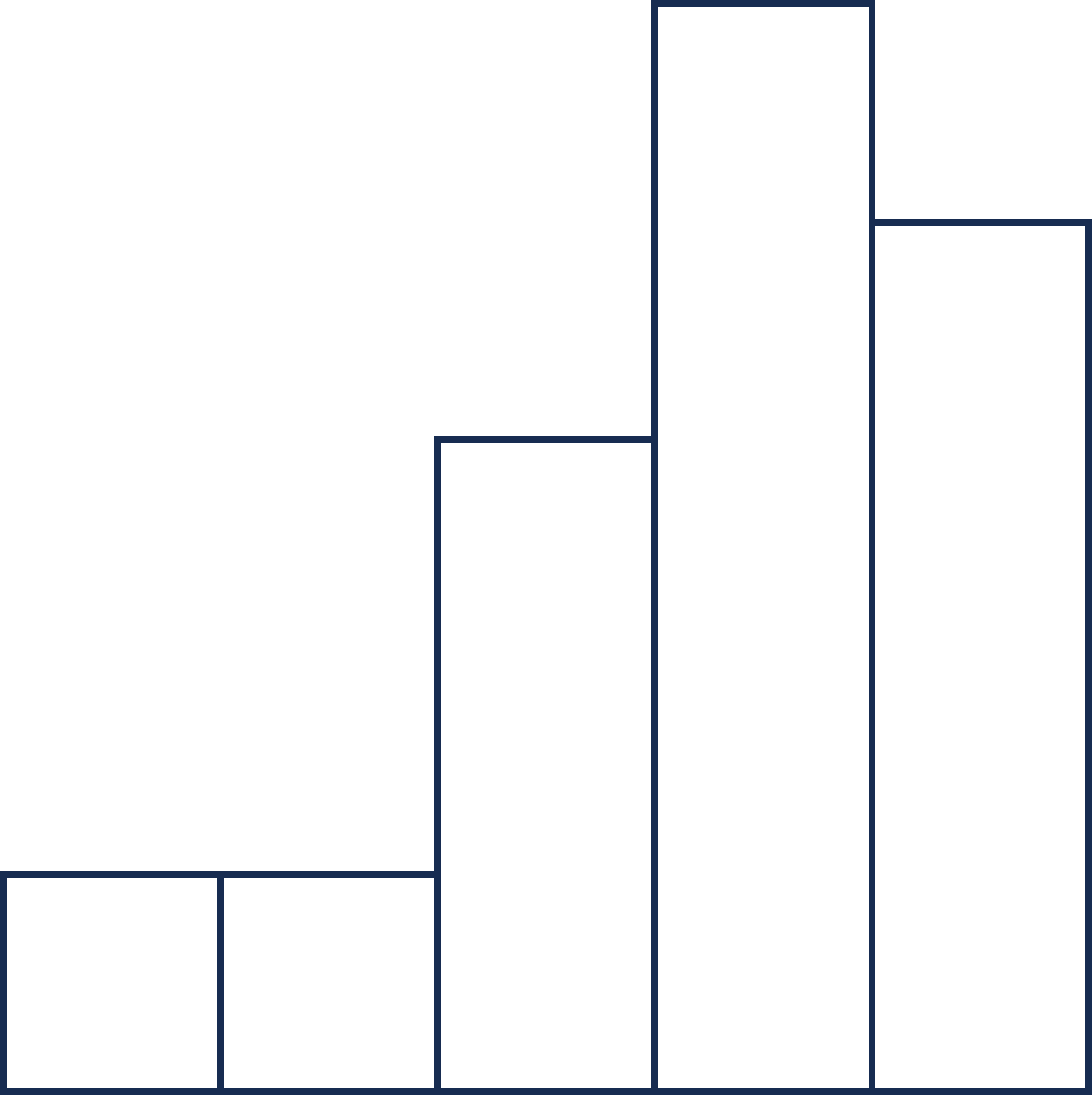
$5$ 개의 직사각형들에서 만들 수 있는 모든 $2$ 개인 쌍은 계단이 된다. 이러한 경우의 수는 $10$ 가지이다. 아래 그림에 두 가지 예를 보였다.

$3$ 개의 직사각형으로 만들 수 있는 계단은 아래 $2$ 가지 경우가 있다. $4$ 개 이상의 직사각형으로 만들 수 있는 계단은 존재하지 않으므로, 답은 $12$이다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설