개미

$N$개의 방이 있는 개미집이 있다. 각 방에는 $1$번부터 $N$번까지 서로 다른 번호가 붙어 있다. 서로 다른 $2$개의 방을 잇는 굴이 $N - 1$개가 있다. 임의의 방에서 임의의 다른 방으로 하나 이상의 굴을 통해서 이동하는 것이 가능하다.

초기에 $i$번 방에는 $A_i$마리의 개미가 있다. 모든 방의 개미의 마리 수를 합하면 $N$, $N+1$, $N+2$ 중 하나의 값이 된다.

많은 수의 개미가 한 방에 모인 경우 생활 환경이 좋지 않기 때문에 각 방에 있는 개미의 수를 제한하고자 한다. 구체적으로, 모든 방에 있는 개미의 수가 $1$ 혹은 $2$가 되게 하는 것이 목표이다. 개미들은 굴을 따라 다른 방으로 자유롭게 이동할 수 있다. 각 개미가 이동한 거리는 거쳐간 굴의 개수로 정의된다.

목표를 달성하기 위해 개미들이 이동해야 하는 거리의 총합의 최소값을 구하는 프로그램을 작성하라.

입력 형식

첫 줄에 방의 개수를 나타내는 정수 $N$이 주어진다. $(2 \le N \le 500\,000)$

그다음 줄에 초기에 각 방에 있는 개미의 마리 수를 나타내는 $N$개의 정수 $A_1, A_2, \cdots, A_N$이 공백으로 구분되어 차례대로 주어진다. ($A_i \ge 0$; $A_1 + A_2 + \cdots + A_N$은 $N$, $N + 1$, $N + 2$ 중 하나와 같다.)

그다음 $N - 1$개의 줄에 걸쳐, 모든 굴의 정보가 주어진다. 각 줄에는 각 굴이 잇는 서로 다른 $2$개의 방 번호가 공백으로 구분되어 주어진다.

출력 형식

첫 줄에 개미들의 이동 거리의 총합의 최솟값을 출력한다.

예제 1

5
0 1 2 0 2
1 2
1 3
2 4
2 5

3

예제 2

5
0 0 2 4 1
1 2
2 3
3 4
4 5

5

예제 설명

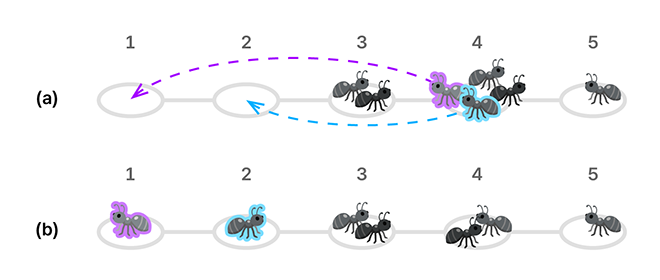
아래 그림은 두 번째 예제를 나타낸다. 각 방 위의 값은 방 번호이다. 그림의 (a) 는 초기에 각 방에 있는 개미의 수를 보여 준다. 그림의 (a) 에서 화살표는 목표를 달성하기 위해 개미 $2$마리가 이동한 것을 보여준다. 개미들이 이동을 마치고 나면 그림의 (b) 와 같이 되어 목표가 달성된다. 두 마리의 개미가 이동한 거리의 총합은 $5$이다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설