물 뿌리기

$N$개의 구역이 길이가 $1$인 $N - 1$개의 도로로 연결되어 있다. 각 구역에는 $1$ 이상 $N$ 이하인 서로 다른 정수로 번호가 매겨져 있고, 어떤 두 구역을 고르더라도 도로를 통해서 연결되어 있다. 이제 여러분은 총 $M$번의 물 뿌리기 작업을 하려고 한다.

한 번의 물 뿌리기 작업은 $(t, u, v, r_u, r_v)$ $5$개의 값으로 정의할 수 있다. 이는 시각 $t$에, $u$번 구역으로부터 $r_u$개 이하의 도로를 통해 갈 수 있으면서 동시에 $v$번 구역으로부터 $r_v$개 이하의 도로를 통해 갈 수 있는 모든 구역에 물을 뿌린다는 뜻이다. 엄밀히 말하면, 시각 $t$에 $u$번 구역으로부터 거리가 $r_u$ 이하인 구역들의 집합과 $v$번 구역으로부터 거리가 $r_v$ 이하인 구역들의 집합의 교집합에 해당하는 구역들에 물을 뿌린다.

또한, 물이 뿌려진 구역에서는 $K$시간 후 인접한 구역으로 물이 전파되며, 전파된 구역 역시 동일하게 $K$시간마다 인접한 구역으로 물을 전파한다.

여러분은 각 구역에 대해 물이 뿌려지거나 전파되는 최초의 시각을 구해야 한다.

$N = 4$, $M = 1$, $K = 1$이고 구역과 도로가 아래의 그림과 같은 예제를 생각해보자.

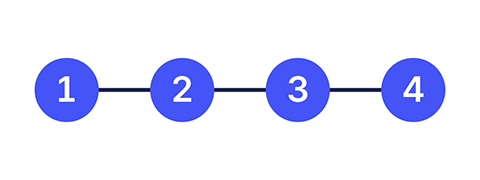
• 먼저 한 번의 물 뿌리기 작업이 $(1, 1, 4, 2, 2)$이라고 하자.
  • 시각 $t = 1$ 때, $1$번 구역에서 거리가 $2$ 이내인 동시에 $4$번 구역에서 거리가 $2$ 이내인, $2$번과 $3$번 구역에 물이 뿌려진다.
  • $K = 1$시간 후인 시각 $t=2$ 때, $2$번 구역 인접한 $1$번 구역에, $3$번 구역과 인접한 $4$번 구역에 물이 뿌려진다.
• 그렇지 않고, 물 뿌리기 작업이 $(1, 1, 4, 1, 1)$이라고 하자.
  • 시각 $t = 1$ 때, $1$번 구역에서 거리가 $1$ 이내인 동시에 $4$번 구역에서 거리가 $1$ 이내인 구역은 없기 때문에, 물이 뿌려지는 구역은 없다.
  • 물이 뿌려진 구역이 없기 때문에 전파되는 구역도 없다.

입력 형식

첫 줄에 구역의 수 $N$, 물뿌리기 작업의 수 $M$, 물이 전파되는데 걸리는 시간을 나타내는 정수 $K$가 공백으로 구분되어 주어진다. ($2 \le N \le 100\,000;$ $1 \le M \le 200\,000;$ $1 \le K \le 50$)

그다음 줄부터 $N - 1$개의 줄에 걸쳐, 각 줄에 각 간선이 연결하는 구역의 번호를 나타내는 두 정수 $U_i$, $V_i$가 공백으로 구분되어 주어진다. ($1 \le U_i, V_i \le N;$ $U_i \ne V_i$)

그다음 줄부터 $M$개의 줄에 걸쳐, 각 줄에 각 물 뿌리기 작업을 나타내는 다섯 개의 정수 $t$, $u$, $v$, $r_u$, $r_v$가 공백으로 구분되어 차례대로 주어진다. ($1 \le t \le 5\,000\,000;$ $1 \le u, v \le N;$ $0 \le r_u, r_v \le N$)

출력 형식

첫 줄부터 $N$개의 줄에 걸쳐 정답을 출력한다.

만약 $i$번 구역에 물이 뿌려지거나 전파된다면, $i$번째 줄에 그 최초의 시각을 출력한다. 그렇지 않는다면, $-1$을 출력한다.

예제 1

4 1 1
1 2
2 3
3 4
1 1 4 2 2

2
1
1
2

예제 2

4 1 1
1 2
2 3
3 4
1 1 4 1 1

-1
-1
-1
-1

예제 3

7 2 2
1 2
2 3
2 4
1 5
5 6
6 7
2 1 2 2 1
1 2 7 3 3

1
2
2
2
1
1
3

예제 설명

입력 예제 1에서, $1$번 방과 $2$번 방을 연결하는 복도 위에 몬스터가 있는 방을 하나 추가하면 문제의 조건을 만족한다.

입력 예제 2에서는 이미 문제의 조건을 만족하여 방을 추가할 필요가 없다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설