트리의 모든 부분 트리의 크기 합

다음과 같이 트리를 만들자. 먼저 $0$번 정점을 루트로 두자. 그 다음, $1 \le i \le N - 1$인 모든 정수 $i$에 대해 작은 수부터 차례대로, $i$번 정점을 $\displaystyle \left\lfloor \frac{i - 1}{K} \right\rfloor$번 정점의 자식 정점으로 두자. 여기서, $\displaystyle \left\lfloor \frac{i - 1}{K} \right\rfloor$는 $i - 1$을 $K$로 나눈 몫을 뜻한다. 이러한 트리는 $0$번부터 $N - 1$번까지 총 $N$개의 정점을 가지며, 모든 정점은 최대 $K$개의 자식 정점을 갖는다.

이제 우리는 이 트리의 각 정점마다, 이 정점이 루트가 되는 부분 트리의 크기를 생각해 보려고 한다. 트리의 크기는 이 트리에 포함되는 정점의 개수이다.

예를 들어, 아래와 같이 $N = 5; K = 2$인 경우의 트리를 생각해 보자.

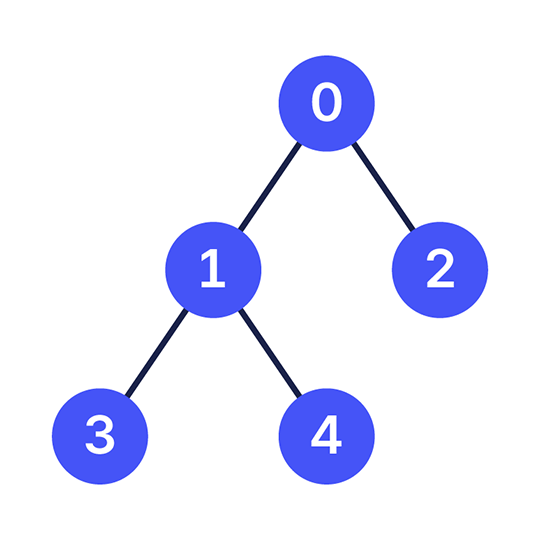
각 정점마다 이 정점이 루트가 되는 부분 트리의 크기는 다음과 같다.

• $0$번 정점이 루트가 되는 부분 트리의 크기는 $5$이다.
• $1$번 정점이 루트가 되는 부분 트리의 크기는 $3$이다.
• $2$, $3$, $4$번 정점이 루트가 되는 부분 트리의 크기는 $1$이다.

따라서, 각각의 정점이 루트가 되는 부분 트리의 크기의 합은 $5 + 3 + 1 + 1 + 1 = 11$이다.

이 값이 매우 커질 수 있으므로, 우리는 이 값을 $P$로 나눈 나머지를 알고 싶다.

$N, K , P$가 주어졌을 때, 각각의 정점이 루트가 되는 부분 트리의 크기의 합을 $P$로 나눈 나머지를 구하는 프로그램을 작성하라.

입력 형식

첫 줄에 테스트 케이스의 수를 나타내는 정수 $T$가 주어진다. ($1 \le T \le 250\,000$)

그다음 $T$줄 각각마다 테스트케이스에 대한 정보가 주어진다. 각 줄에는 트리의 정점 수, 정점의 최대 자식 수, 나누는 수를 나타내는 세 정수 $N, K , P$가 공백으로 구분되어 차례대로 주어진다. ($1 \le N, K \le 10^{18};$ $1 \le P \le 1\,000\,000\,000$)

출력 형식

각 테스트 케이스의 결과를 한 줄에 출력한다. 출력은 테스트 케이스에서 주어진 트리의 각 정점이 루트가 되는 서브트리의 크기의 총합을 주어진 $P$로 나눈 나머지이다.

예제 1

1
5 2 17

11

예제 2

3
13 3 37
13 3 13
13 3 5

34
8
4

예제 설명

• 예제 1에 대한 설명은 문제 본문에 주어져 있다.
• 예제 2에서는 첫 레벨에 정점 $1$개, 둘째 레벨에 정점 $3$개, 셋째 레벨에 정점 $9$개가 있다.
  • 첫 레벨에 있는 정점이 루트가 되는 서브트리의 크기의 합은 $1 \times (1+3+9) = 13$,
  • 둘째 레벨에 있는 정점이 루트가 되는 서브트리의 크기의 합은 $3 \times (1+3) = 12$,
  • 셋째 레벨에 있는 정점이 루트가 되는 서브트리의 크기의 합은 $9 \times 1 = 9$.
  • 따라서, 총합은 $13 + 12 + 9 = 34$이며, 이를 각각 $37$, $13$, $5$로 나눈 나머지는 각각 $34$, $8$, $4$이다.

채점 방식

입력 케이스들은 다음과 같은 종류로 구별되며, 한 종류의 케이스를 다 맞혀야 그 종류에 배정된 점수를 받을 수 있다.

해설